
【题目】如图,在边长为2的正方形ABCD中,P是BC边上一动点(点P不与B、C重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA、NA,则以下结论:①△CMP∽△BPA;②四边形AMCB的面积最大值为2.5;③△ADN≌△AEN;④线段AM的最小值为2.5;⑤当P为BC中点时,AE为线段NP的中垂线.正确的有_____(只填序号)

【答案】①②③④
【解析】分析:①正确.只要证明∠CPM=∠PAB,∠C=∠B=90°,即可;
②正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可;
③正确.根据HL即可证明;
④正确,作MG⊥AB于G,因为AM=![]() ,所以AG最小时AM最小,构建二次函数,求得AG的最小值为
,所以AG最小时AM最小,构建二次函数,求得AG的最小值为![]() ,AM的最小值为
,AM的最小值为![]() .
.
⑤错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
详解:①由翻折可知,∠APE=∠APB,∠MPC=∠MPN,
∴∠APE+∠MPF=![]() ∠CPN+
∠CPN+![]() ∠BPE=90°,
∠BPE=90°,
∴∠CPM+∠APB=90°,∵∠APB+∠PAB=90°,
∴∠CPM=∠PAB,∵∠C=∠B=90°,
∴△CMP∽△BPA.故①正确;
②设PB=x,则CP=2-x,
∵△CMP∽△BPA,
∴![]() ,,
,,
∴CM=![]() x(2-x),
x(2-x),
∴S四边形AMCB=![]() [2+
[2+![]() x(2-x)]×2=-
x(2-x)]×2=-![]() x2+x+2=-
x2+x+2=-![]() (x-1)2+2.5,
(x-1)2+2.5,
∴x=1时,四边形AMCB面积最大值为2.5,故②正确;
③在Rt△ADN和Rt△AEN中,
![]() ,
,
∴△ADN≌△AEN.故③正确;
④作MG⊥AB于G,
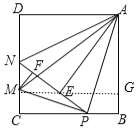
∵AM=![]() ,
,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=2-![]() x(2-x)=
x(2-x)=![]() (x-1)2+
(x-1)2+![]() ,
,
∴x=1时,AG最小值=![]() ,
,
∴AM的最小值=![]() ,故④正确.
,故④正确.
⑤当PB=PC=PE=1时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+1)2=(2-y)2+12解得y=![]()
∴NE=![]() ,
,
∴NE≠EP,故⑤错误,


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点在格点上.
(1)作出与△ABC关于x轴对称的图形△A1B1C1;
(2)求出A1,B1,C1三点坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
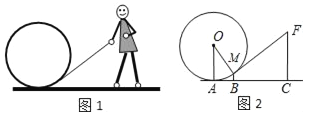
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD分别与AE、AF相交于G、H.

(1)在图中找出与△ABE相似的三角形,并说明理由;
(2)若AG=AH,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一玩具工厂用于生产的全部劳力为450个工时,原料为400个单位.生产一个小熊要使用15个工时、20个单位的原料,售价为80元;生产一个小猫要使用10个工时、5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产小熊、小猫的个数,可以使小熊和小猫的总售价尽可能高.请用你所学过的数学知识分析,总售价是否可能达到2200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)在图中的点上标出相应字母A、B、C,并求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在□ABCD中,点G为对角线AC的中点,过点G的直线EF分别交边AB、CD于点E、F,过点G的直线MN分别交边AD、BC于点M、N,且∠AGE=∠CGN.

(1)求证:四边形ENFM为平行四边形;
(2)当四边形ENFM为矩形时,求证:BE=BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明从点A出发,前进10m后向右转20°,再前进10m后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.
(1)小明一共走了多少米?
(2)这个多边形的内角和是多少度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com