练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，E点为DF上的点，B为AC上的点，∠1＝∠2，∠C＝∠D，那么DF∥AC，请完成它成立的理由

    ∵∠1＝∠2，∠2＝∠3 ，∠1＝∠4（ ）

    ∴∠3＝∠4（ ）

    ∴________∥_______ （ ）

    ∴∠C＝∠ABD（ ）

    ∵∠C＝∠D（ ）

    ∴∠D＝∠ABD（ ）

    ∴DF∥AC（ ）

    【答案】对顶角相等，CE，BD，内错角相等，两直线平行，两直线平行，同位角相等

    【解析】

    此题主要利用对顶角相等，得出∠2=∠3，∠1=∠4，然后等量代换得出∠3=∠4；根据内错角相等，两直线平行，得出BD∥CE，再根据平行线的性质：两直线平行，同位角相等，得出∠C=∠ABD，然后证出∠D=∠ABD，进而证得DF∥AC．

    ∵∠1＝∠2，（ 已知 ）

    又∵∠2＝∠3 ，∠1＝∠4（ 对顶角相等 ）

    ∴∠3＝∠4（ 等量代换 ）

    ∴_____BD___∥__CE_____（ 内错角相等，两直线平行 ）

    ∴∠C＝∠ABD（ 两直线平行，同位角相等 ）

    ∵∠C＝∠D（已知 ）

    ∴∠D＝∠ABD（等量代换 ）

    ∴DF∥AC（ 内错角相等，两直线平行 ）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上，点A表示1，现将点A沿数轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第2次从点A1向右移动6个单位长度到达点A2，第3次从点A2向左移动9个单位长度到达点A3，…，按照这种移动规律进行下去，第n次移动到达点An，如果点An与原点的距离不小于50，那么n的最小值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图17，在△ABC中，D是BC边上的一点，E是AD的中点，过A作BC的平行线交CE的延长线于F，且AF＝BD，连接BF.

    (1)求证：BD＝CD.

    (2)如果AB＝AC，试判断四边形AFBD的形状，并证明你的结论．

    (3)当△ABC满足什么条件时，四边形AFBD为正方形？(写出条件即可，不要求证明)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，A、B两点之间的距离是90米，甲、乙两机器人分别从A、B两点同时同向出发到终点C，乙机器人始终以50米分的速度行走，乙行走9分钟到达C点．设两机器人出发时间为t（分钟），当t＝3分钟时，甲追上乙．

    请解答下面问题：

    （1）B、C两点之间的距离是　 　米．

    （2）求甲机器人前3分钟的速度为多少米/分？

    （3）若前4分钟甲机器人的速度保持不变，在4≤t≤6分钟时，甲的速度变为与乙相同，求两机器人前6分钟内出发多长时间相距28米？

    （4）若6分钟后甲机器人的速度又恢复为原来出发时的速度，直接写出当t＞6时，甲、乙两机器人之间的距离S．（用含t的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

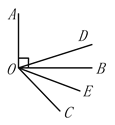
    【题目】如图，DO平分∠AOC，OE平分∠BOC，若OA⊥OB，

    （1）当∠BOC＝30°，∠DOE＝_______________； 当∠BOC＝60°，∠DOE＝_______________；

    （2）通过上面的计算，猜想∠DOE的度数与∠AOB有什么关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等腰三角形ABC中，AB=AC，点D、E分别在边AB、AC上，且AD=AE，连接BE、CD，交于点F．

    （1）判断∠ABE与∠ACD的数量关系，并说明理由；

    （2）求证：过点A、F的直线垂直平分线段BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某同学在平时的练习中，遇到下面一道题目：

    如图，∠AOC=90°，OE 平分∠BOC，OD平分∠AOB.

    ①若∠BOC=60°，求∠DOE 度数；

    ②若∠BOC=α（0＜α＜90°），其他条件不变，求∠DOE 的度数.

    （1）下面是某同学对①问的部分解答过程，请你补充完整.

    ∵OE 平分∠BOC，∠BOC=60°

    ∴∠BOE= . (角平分线的定义)

    ∵∠AOC=90°，∠BOC=60°

    ∴ ，

    ∵OD 平分∠AOB，

    ∴ ，(角平分线的定义)

    ∴∠DOE= .

    （注：符号∵表示因为，用符号∴表示所以）.

    （2）仿照①的解答过程，完成第②小题.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若直线y=3x+m经过第一、三、四象限，则抛物线y=（x-m） +1的顶点在第象限（ ）
    A.一
    B.二
    C.三
    D.四

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读与思考：

    整式乘法与因式分解是方向相反的变形，由 ，

    可得 ．

    利用这个式子可以将某些二次项系数是1的二次三项式分解因式．

    例如：将式子分解因式．

    这个式子的常数项，一次项系，

    所以．

    解： ．

    上述分解因式的过程，也可以用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数（如右图）.

    请仿照上面的方法，解答下列问题：

    （1）分解因式：＝___________________；

    （2）若可分解为两个一次因式的积，则整数P的所有可能值是________．

    查看答案和解析>>

    同步练习册答案