
【题目】如图5,O为直线AB上一点, ∠AOC=48°,OE平分∠AOC, ∠DOE=90°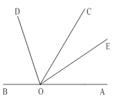
(1)求∠BOE的度数。
(2)试判断OD是否平分∠BOC?试说明理由。
【答案】
(1)解: ∵OE平分∠AOC,∴∠AOE=∠EOC= ![]() ∠AOC=
∠AOC= ![]() ×48°=24°,∴∠BOE=180°-∠AOE=180°-24°=156°
×48°=24°,∴∠BOE=180°-∠AOE=180°-24°=156°
(2)解: OD平分∠BOC.理由如下:
∵∠DOE=90°,∠EOC=24°,∴∠DOC =∠DOE -∠EOC =90°-24°=66°.
∵∠BOD =∠BOE-∠DOE=156°-90°=66°,∴∠DOC=∠BOD ,∴OD平分∠BOC
【解析】(1)根据角平分线的定义得出∠AOE=∠EOC= ![]() ∠AOC=24° ,然后根据邻补角的定义得出答案;
∠AOC=24° ,然后根据邻补角的定义得出答案;
(2)OD平分∠BOC.理由如下: 根据角的和差得出∠DOC =∠DOE -∠EOC =90°-24°=66° ,∠BOD =∠BOE-∠DOE=156°-90°=66° ,从而得出∠DOC=∠BOD ,即OD平分∠BOC 。


科目:初中数学 来源: 题型:
【题目】在线段、平行四边形、矩形、等腰三角形、正六边形、圆这几个图形中,既是轴对称图形又是中心对称图形的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A钟礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州素有“鱼米之乡”的美称,某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售,按计划20辆汽车都要装运,每辆汽车只能装运同一种鱼,且必须装满,根据下表提供的信息,解答以下问题:

(1)设装运鲢鱼的车辆为x辆,装运草鱼的车辆为y辆,求y与x之间的函数关系式;
(2)如果装运每种鱼的车辆都不少于2辆,那么怎样安排车辆能使此次销售获利最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,AB=AC,AD是△ABC的角平分线,EF垂直平分AC,分别交AC,AD,AB于点E,M,F.若∠CAD=20°,求∠MCD的度数.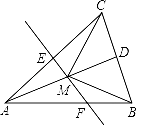
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com