
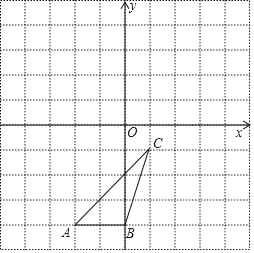
【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).
(1)在图中画出△ABC关于原点对称的△A1B1C1;
(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求点A运动路径长.
科目:初中数学 来源: 题型:
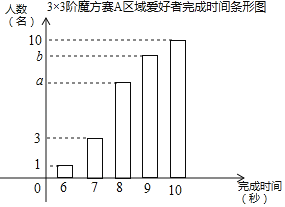
【题目】(2017湖南株洲第21题)某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:
①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).
②若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数.
③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
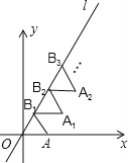
【题目】如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
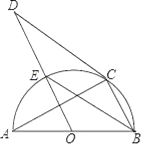
A. AC⊥BCB. BE平分∠ABCC. BE∥CDD. ∠D=∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于天气炎热,某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在_______分钟内,师生不能呆在教室.
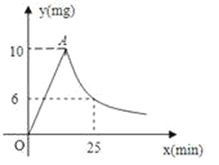
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
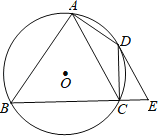
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动速度为lcm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),当t=4时,求y的值.
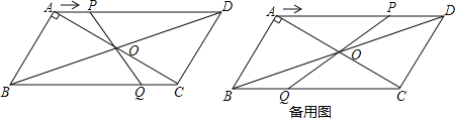
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(![]() ,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
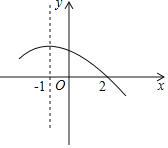
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
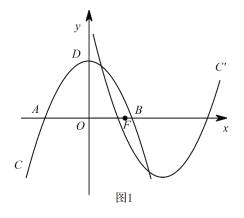
【题目】如图1,在平面直角坐标系xOy中,抛物线C:y=ax2+bx+c与x轴相交于A,B两点,顶点为D(0,4),AB=4![]() ,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
,设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C/.
(1)求抛物线C的函数表达式;
(2)若抛物线C/与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围.
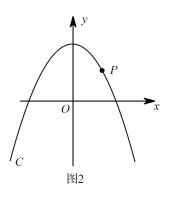
(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C/上的对应点P/,设M是C上的动点,N是C/上的动点,试探究四边形PMP/N能否成为正方形?若能,请直接写出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com