
【题目】已知λ∈R,函数f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的导数为g(x).
(1)求曲线y=f(x)在x=1处的切线方程;
(2)若函数g(x)存在极值,求λ的取值范围;
(3)若x≥1时,f(x)≥0恒成立,求λ的最大值.
【答案】
(1)解:)f(x)=ex﹣ex﹣λ(xlnx﹣x+1)的定义域为(0,+∞).
f′(x)=ex﹣e﹣λlnx,f′(1)=0,又f(1)=0.
曲线y=f(x)在x=1处的切线方程为y=0
(2)解:∵g(x)=f′(x)=ex﹣e﹣λlnx,(x>0),g′(x)= ![]()
函数g(x)存在极值,即方程 ![]() 有正实数根,
有正实数根,
λ=xex,(x>0),
令G(x)=xex,G′(x)=x(ex+1)>0在(0,+∞)恒成立.
x∈(0,+∞)时,G(x)>0,
∴函数g(x)存在极值,λ的取值范围为(0,+∞)
(3)解:由(1)、(2)可知f(1)=0,f′(1)=g(1)=0
结合(2)x≥1时,g′(x)= ![]() ≥0,可得λ≤xex,(x≥1),
≥0,可得λ≤xex,(x≥1),
G(x)=xex,在(1,+∞)恒成立.
∴λ≤e时,g′(x)≥0,g(x)在[1,+∞)递增,g(x)≥g(1)=0
故f(x)在[1,+∞)递增,∴f(x)≥f(1)=0.
当λ>e时,存在x0>1,使g′(x)=0,∴x∈(1,x0)时,g′(x)<0,
即x∈(1,x0)时,g(x)递减,而g(1)=0,
∴x∈(1,x0)时,g(x)<0,此时f(x)递减,而f(1)=0,
∴在(1,x0),f(x)<0,故当λ>e时,f(x)≥0不恒成立;
综上x≥1时,f(x)≥0恒成立,λ的最大值为e
【解析】(1)求出f′(x)=ex﹣e﹣λlnx,f′(1)=0,又f(1)=0,得到曲线y=f(x)在x=1处的切线方程为y=0.(2)g(x)=f′(x)=ex﹣e﹣λlnx(x>0),g′(x)= ![]() ,函数g(x)存在极值,即方程
,函数g(x)存在极值,即方程 ![]() 有正实数根,λ=xex , (x>0),可得λ的取值范围.(3)由(1)、(2)可知f(1)=0,f′(1)=g(1)=0,结合(2)分λ≤e,λ>e,讨论x≥1时,是否f(x)≥0恒成立,即可.
有正实数根,λ=xex , (x>0),可得λ的取值范围.(3)由(1)、(2)可知f(1)=0,f′(1)=g(1)=0,结合(2)分λ≤e,λ>e,讨论x≥1时,是否f(x)≥0恒成立,即可.
【考点精析】本题主要考查了函数的极值与导数和函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值;求函数
是极小值;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c+2=0无实数根;③a﹣b+c≥0; ④ ![]() 的最小值为3.其中正确的是( )
的最小值为3.其中正确的是( )
A.①②③
B.②③④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△OPA和△OQB分别是以OP、OQ为直角边的等腰直角三角形,点C、D、E分别是OA、OB、AB的中点.
(1)当∠AOB=90°时如图1,连接PE、QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,当∠AOB是锐角时如图2,(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,当∠AOB为钝角时,延长PC、QD交于点G,使△ABG为等边三角形如图3,求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF. 
(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD=DF=FB,DE∥FG∥BC,且把三角形ABC分成面积为S1 , S2 , S3三部分,则S1:S2:S3=( ) 
A.1:2:3
B.1:4:9
C.1:3:5
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=﹣ ![]() (x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y=
(x﹣t)(x﹣t+4)(常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线y= ![]() (k>0,x>0)于点P,且OAMP=12.
(k>0,x>0)于点P,且OAMP=12.
(1)求k的值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.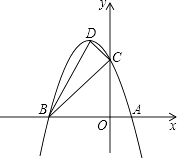
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P,A,C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,E为BC边上一点,G为BC延长线上一点,过点E作∠AEM=60°,交∠ACG的平分线于点M.
(1)如图(1),当点E在BC边的中点位置时,通过测量AE,EM的长度,猜想AE与EM满足的数量关系是;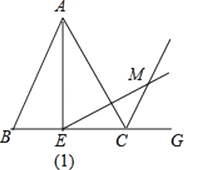
(2)如图(2),小晏通过观察、实验,提出猜想:当点E在BC边的任意位置时,始终有AE=EM.小晏把这个猜想与同学进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:在BA上取一点H使AH=CE,连接EH,要证AE=EM,只需证△AHE≌△ECM.
想法2:找点A关于直线BC的对称点F,连接AF,CF,EF.(易证∠BCF+∠BCA+ACM=180°,所以M,C,F三点在同一直线上)要证AE=EM,只需证△MEF为等腰三角形.
想法3:将线段BE绕点B顺时针旋转60°,得到线段BF,连接CF,EF,要证AE=EM,只需证四边形MCFE为平行四边形.
请你参考上面的想法,帮助小晏证明AE=EM.(一种方法即可)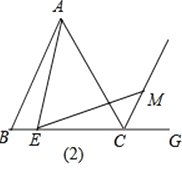
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com