
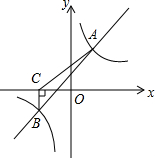
 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.分析 (1)将点A坐标代入y=$\frac{m}{x}$可得反比例函数解析式,据此求得点B坐标,根据A、B两点坐标可得直线解析式;
(2)根据点B坐标可得底边BC=2,由A、B两点的横坐标可得BC边上的高,据此可得.
解答 解:(1)将点A(2,4)代入y=$\frac{m}{x}$,得:m=8,
则反比例函数解析式为y=$\frac{8}{x}$,
当x=-4时,y=-2,
则点B(-4,-2),
将点A(2,4)、B(-4,-2)代入y=kx+b,
得:$\left\{\begin{array}{l}{2k+b=4}\\{-4k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
则一次函数解析式为y=x+2;
(2)由题意知BC=2,
则△ACB的面积=$\frac{1}{2}$×2×6=6.
点评 本题主要考查一次函数与反比例函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积求法是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
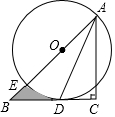 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
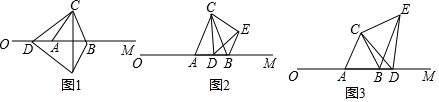
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正六边形的外角和等于360° | B. | 位似图形必定相似 | ||
| C. | 样本方差越大,数据波动越小 | D. | 方程x2+x+1=0无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
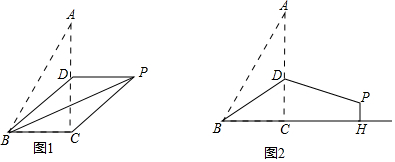
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com