Question

如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）．

（1）图2中的阴影部分的面积为______；
（2）观察图2请你写出 （a+b）²、（a-b）²、ab之间的等量关系是______；
（3）根据（2）中的结论，若x+y=5，x•y=，则x-y=______；
（4）实际上通过计算图形的面积可以探求相应的等式．如图3，你有什么发现？______．

Answer 1

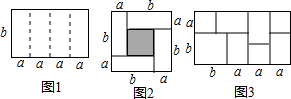
解：（1）阴影部分为边长为（b-a）的正方形，所以阴影部分的面积（b-a）²；
（2）图2中，用边长为a+b的正方形的面积减去边长为b-a的正方形等于4个长宽分别a、b的矩形面积，
所以（a+b）²-（a-b）²=4ab；
（3）∵（x+y）²-（x-y）²=4xy，
而x+y=5，x•y=，
∴5²-（x-y）²=4×，
∴（x-y）²=16，
∴x-y=±4；
（4）边长为（a+b）与（3a+b）的矩形面积为（a+b）（3a+b），它由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成，
∴（a+b）•（3a+b）=3a²+4ab+b²．
故答案为（b-a）²；（a+b）²-（a-b）²=4ab；±4；（a+b）•（3a+b）=3a²+4ab+b²．
分析：（1）阴影部分为边长为（b-a）的正方形，然后根据正方形的面积公式求解；
（2）在图2中，大正方形有小正方形和4个矩形组成，则（a+b）²-（a-b）²=4ab；
（3）由（2）的结论得到（x+y）²-（x-y）²=4xy，再把x+y=5，x•y=得到（x-y）²=16，然后利用平方根的定义求解；
（4）观察图形得到边长为（a+b）与（3a+b）的矩形由3个边长为a的正方形、4个边长为a、b的矩形和一个边长为b的正方形组成，则有（a+b）•（3a+b）=3a²+4ab+b²．
点评：本题考查了完全平方公式的几何背景：利用面积法证明完全平方公式（a-b）2=a²-2ab+b²．