
”¾ĢāÄæ”æŌŚĻÖ½ń”°»„ĮŖĶų+”±µÄŹ±“ś£¬ĆÜĀėÓėĪŅĆĒµÄÉś»īŅŃ¾½ōĆÜĻąĮ¬£¬Ćܲ»æÉ·Ö£®¶ųÖīČē”°123456”±”¢ÉśČÕµČ¼ņµ„ĆÜĀėÓÖČŻŅ×±»ĘĘ½ā£¬Ņņ“ĖĄūÓĆ¼ņµ„·½·Ø²śÉśŅ»×éČŻŅ×¼ĒŅäµÄ6Ī»ŹżĆÜĀė¾ĶŗÜÓŠ±ŲŅŖĮĖ£®ÓŠŅ»ÖÖÓĆ”°ŅņŹ½·Ö½ā·Ø²śÉśµÄĆÜĀė£¬·½±ć¼ĒŅ䣬ĘäŌĄķŹĒ£ŗ½«Ņ»øö¶ąĻīŹ½·Ö½āŅņŹ½£¬Čē¶ąĻīŹ½£ŗx3+2x2©x©2ŅņŹ½·Ö½āµÄ½į¹ūĪŖ£Øx©1£©£Øx+1£©£Øx+2£©£¬µ±x£½18Ź±£¬x©1£½17£¬x+1£½19£¬x+2£½20£¬“ĖŹ±æÉŅŌµĆµ½Źż×ÖĆÜĀė171920£®
£Ø1£©øł¾ŻÉĻŹö·½·Ø£¬µ±x£½21£¬y£½7Ź±£¬¶ŌÓŚ¶ąĻīŹ½x3©xy2·Ö½āŅņŹ½ŗóæÉŅŌŠĪ³ÉÄÄŠ©Źż×ÖĆÜĀė£æ£ØŠ“³öĮ½øö£©
£Ø2£©Čō¶ąĻīŹ½x3+£Øm©3n£©x2©nx©21ŅņŹ½·Ö½āŗó£¬ĄūÓƱ¾ĢāµÄ·½·Ø£¬µ±x£½27Ź±æÉŅŌµĆµ½ĘäÖŠŅ»øöĆÜĀėĪŖ242834£¬Ēóm”¢nµÄÖµ£®
”¾“š°ø”æ£Ø1£©æÉŅŌŠĪ³ÉµÄŹż×ÖĆÜĀėŹĒ£ŗ212814”¢211428£»£Ø2£©mµÄÖµŹĒ56£¬nµÄÖµŹĒ17£®
”¾½āĪö”æ
£Ø1£©ĻČ½«¶ąĻīŹ½½ųŠŠŅņŹ½·Ö½ā£¬Č»ŗóŌŁøł¾ŻŹż×ÖĆÜĀė·½·ØŠĪ³ÉŹż×ÖĆÜĀė¼“æÉ£»£Ø2£©Éčx3+£Øm©3n£©x2©nx©21£½£Øx+p£©£Øx+q£©£Øx+r£©£¬µ±x£½27Ź±æÉŅŌµĆµ½ĘäÖŠŅ»øöĆÜĀėĪŖ242834£¬µĆµ½·½³Ģ½ā³öp”¢q”¢r£¬Č»ŗó»Ų“śČėŌ¶ąĻīŹ½¼“æÉĒóµĆm”¢n
£Ø1£©x3©xy2£½x£Øx2©y2£©£½x£Øx+y£©£Øx©y£©£¬
µ±x£½21£¬y£½7Ź±£¬x+y£½28£¬x©y£½14£¬
”ąæÉŅŌŠĪ³ÉµÄŹż×ÖĆÜĀėŹĒ£ŗ212814”¢211428£»
£Ø2£©Éčx3+£Øm©3n£©x2©nx©21£½£Øx+p£©£Øx+q£©£Øx+r£©£¬
”ßµ±x£½27Ź±æÉŅŌµĆµ½ĘäÖŠŅ»øöĆÜĀėĪŖ242834£¬
”ą27+p£½24£¬27+q£½28£¬27+r£½34£¬
½āµĆ£¬p£½©3£¬q£½1£¬r£½7£¬
”ąx3+£Øm©3n£©x2©nx©21£½£Øx©3£©£Øx+1£©£Øx+7£©£¬
”ąx3+£Øm©3n£©x2©nx©21£½x3+5x2©17x©21£¬
”ą ![]() µĆ£¬
µĆ£¬![]()
¼“mµÄÖµŹĒ56£¬nµÄÖµŹĒ17£®


 ĆūŹ¦µ¼ŗ½µ„ŌŖĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
ĆūŹ¦µ¼ŗ½µ„ŌŖĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø ĆūŠ£Ćū¾ķµ„ŌŖĶ¬²½ŃµĮ·²āŹŌĢāĻµĮŠ“š°ø
ĆūŠ£Ćū¾ķµ„ŌŖĶ¬²½ŃµĮ·²āŹŌĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCµÄČżøö¶„µć×ų±ź·Ö±šĪŖA£Ø-1£¬3£©£¬B£Ø-2£¬1£©£¬C£Ø-3£¬1£©£®
£Ø1£©¢Ł»³ö”÷ABC¹ŲÓŚyÖį¶Ō³ĘµÄ”÷A1B1C1 £¬ ²¢Š“³öA1µćµÄ×ų±ź¼°sin”ĻB1C1A1µÄÖµ£»
¢ŚŅŌŌµćOĪŖĪ»ĖĘÖŠŠÄ£¬Ī»ĖʱČĪŖ1£ŗ2£¬ŌŚyÖįµÄ×ó²ą£¬»³ö½«”÷ABC·Å“óŗóµÄ”÷A2B2C2 £¬ ²¢Š“³öA2µćµÄ×ų±ź£»
£Ø2£©ČōµćDĪŖĻ߶ĪBCµÄÖŠµć£¬Ö±½ÓŠ“³ö¾¹ż£Ø2£©µÄ±ä»ÆŗóµćDµÄ¶ŌÓ¦µćD2µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Ļ“Ļ”¢Ć÷Ć÷”¢ĮęĮę”¢ĄžĄžĖÄČĖ¹²Ķ¬Ģ½¾æ“śŹżŹ½![]() µÄÖµµÄĒéæöĖūĆĒ×öĮĖČēĻĀ·Ö¹¤£¬“Ļ“ĻøŗŌšÕŅÖµĪŖ0Ź±
µÄÖµµÄĒéæöĖūĆĒ×öĮĖČēĻĀ·Ö¹¤£¬“Ļ“ĻøŗŌšÕŅÖµĪŖ0Ź±![]() µÄÖµ£¬Ć÷Ć÷øŗŌšÕŅÖµĪŖ4Ź±
µÄÖµ£¬Ć÷Ć÷øŗŌšÕŅÖµĪŖ4Ź±![]() µÄÖµ£¬ĮęĮęøŗŌšÕŅ×īŠ”Öµ£¬ĄžĄžøŗŌšÕŅ×ī“óÖµ£¬¼ø·ÖÖÓ£¬ø÷×ŌĶرØĢ½¾æµÄ½įĀŪ£¬ĘäÖŠÕżČ·µÄŹĒ£Ø £©
µÄÖµ£¬ĮęĮęøŗŌšÕŅ×īŠ”Öµ£¬ĄžĄžøŗŌšÕŅ×ī“óÖµ£¬¼ø·ÖÖÓ£¬ø÷×ŌĶرØĢ½¾æµÄ½įĀŪ£¬ĘäÖŠÕżČ·µÄŹĒ£Ø £©
£Ø1£©“Ļ“ĻČĻĪŖÕŅ²»µ½ŹµŹż![]() £¬Ź¹
£¬Ź¹![]() µÄÖµĪŖ0£»
µÄÖµĪŖ0£»
£Ø2£©Ć÷Ć÷ČĻĪŖÖ»ÓŠµ±![]() Ź±£¬
Ź±£¬![]() µÄÖµĪŖ4£»
µÄÖµĪŖ4£»
£Ø3£©ĮęĮę·¢ĻÖ![]() ÓŠ×īŠ”Öµ£»£Ø4£©ĄžĄž·¢ĻÖ
ÓŠ×īŠ”Öµ£»£Ø4£©ĄžĄž·¢ĻÖ![]() ÓŠ×ī“óÖµ
ÓŠ×ī“óÖµ
A.£Ø1£©£Ø2£©B.£Ø1£©£Ø3£©C.£Ø1£©£Ø4£©D.£Ø1£©£Ø2£©£Ø4£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŌŚ”÷ABCÖŠ,”ĻBAC=90”ć,AC=2AB,µćDŹĒACµÄÖŠµć,½«Ņ»æéČń½ĒĪŖ45”ćµÄÖ±½ĒČż½Ē°åADEČēĶ¼·ÅÖĆ,Į¬½ÓBE,EC.ĻĀĮŠÅŠ¶Ļ:¢Ł”÷ABE”Õ”÷DCE;¢ŚBE=EC;¢ŪBE”ĶEC;¢ÜEC=![]() DE.ĘäÖŠÕżČ·µÄÓŠ( )
DE.ĘäÖŠÕżČ·µÄÓŠ( )

A.1øöB.2øöC.3øöD.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDÖŠ£¬AD=4£¬µćEŹĒ¶Ō½ĒĻßACÉĻŅ»µć£¬Į¬½ÓDE£¬¹żµćE×÷EF”ĶED£¬½»ABÓŚµćF£¬Į¬½ÓDF£¬½»ACÓŚµćG£¬½«”÷EFGŃŲEF·ÕŪ£¬µĆµ½”÷EFM£¬Į¬½ÓDM£¬½»EFÓŚµćN£¬ČōµćFŹĒABµÄÖŠµć£¬Ōņ”÷EMNµÄÖܳ¤ŹĒ £® 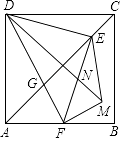
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,ŌŚRt”÷ABCÖŠ,”ĻACB=90”ć,”ĻA=30”ć,CD”ĶAB½»ABÓŚµćE,ĒŅCD=AC,DF”ĪBC,·Ö±šÓėAB,AC½»ÓŚµćG,F.

£Ø1£©ĒóÖ¤:GE=GF£»
£Ø2£©ĢīæÕ£ŗČōBD=1,ŌņDFµÄ³¤ŹĒ .
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»“ĪµŲÕšÖŠ£¬Ä³“åŹÜµŲÕšÓ°ĻģŃĻÖŲ£¬ŅŃ¾³ÉĪŖŅ»Ę¬·ĻŠę.ĪŖÖŲ½Ø¼ŅŌ°£¬Õžø®×¼±øŠŽ½ØŌŚµŲÕšÖŠŹÜĖšµÄŅ»Ģõ¹«Ā·£¬ČōÓɼ׹¤³Ģ¶Óµ„¶ĄŠŽŠč3øöŌĀĶź³É£¬ĆæŌĀŗÄ׏12ĶņŌŖ£»ČōÓÉŅŅ¹¤³Ģ¶Óµ„¶ĄŠŽ½ØŠč6øöŌĀĶź³É£¬ĆæŌĀŗÄ׏5ĶņŌŖ.
£Ø1£©ĒėĪŹČōÓɼה¢ŅŅĮ½¹¤³Ģ¶ÓŗĻ×÷ŠŽ½ØŠč¼øøöŌĀĶź³É£æ¹²ŗÄ׏¶ąÉŁĶņŌŖ£æ
£Ø2£©ČōÓɼה¢ŅŅĮ½¹¤³Ģ¶ÓĻČŗĻ×÷£¬Ź£ĻĀµÄÓÉŅŅ¶ÓĄ“Ķź³É£¬ĒŅĒ”ŗĆĄśŹ±4øöŌĀĶź³ÉŠŽ½ØČĪĪń£¬ĒóÕāŃł°²ÅŹ²ŗÄ׏¶ąÉŁĶņŌŖ£æ£ØŹ±¼ä°“ÕūŌĀ¼ĘĖć£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«Rt”÷ABC£ØĘäÖŠ”ĻB=35”ć£¬”ĻC=90”ć£©ČʵćA°“Ė³Ź±Õė·½ĻņŠż×Ŗµ½”÷AB1C1µÄĪ»ÖĆ£¬Ź¹µĆµćC£¬A£¬B1ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬ÄĒĆ“Šż×Ŗ½ĒµČÓŚ£Ø £© 
A.55”ć
B.70”ć
C.125”ć
D.145”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij¹«Ė¾ÓŠA”¢BĮ½ÖÖŠĶŗŵÄæĶ³µ¹²11Į¾£¬ĖüĆĒµÄŌŲæĶĮæ£Ø²»ŗ¬Ė¾»ś£©”¢ČÕ×ā½š”¢³µĮ¾ŹżČēĻĀ±ķĖłŹ¾£¬ŅŃÖŖÕā11Į¾æĶ³µĀśŌŲŹ±æÉ“īŌŲ³ĖæĶ350ČĖ£®
AŠĶæĶ³µ | BŠĶæĶ³µ | |
ŌŲæĶĮæ£ØČĖ/Į¾£© | 40 | 25 |
ČÕ×ā½š£ØŌŖ/Į¾£© | 320 | 200 |
³µĮ¾Źż£ØĮ¾£© | a | b |
£Ø1£©Ēóa”¢bµÄÖµ£»
£Ø2£©Ä³Š£ĘßÄź¼¶Ź¦ÉśÖÜČÕ¼ÆĢå²Ī¼ÓÉē»įŹµ¼ł£¬¼Ę»®×āÓĆA”¢BĮ½ÖÖŠĶŗŵÄæĶ³µ¹²6Į¾£¬ĒŅ×ā³µ×Ü·ŃÓĆ²»³¬¹ż1700ŌŖ£®
¢Ł×ī¶ąÄÜ×āÓĆAŠĶæĶ³µ¶ąÉŁĮ¾£æ
¢ŚČōĘßÄź¼¶Ź¦Éś¹²195ČĖ£¬Š“³öĖłÓŠµÄ×ā³µ·½°ø£¬²¢Č·¶Ø×īŹ”Ē®µÄ×ā³µ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com