
分析 (1)①设购进A种计算器x台,则购进B种计算器(50-x)台,根据总钱数=购进A种计算机的钱数+购进B种计算机的钱数即可列出关于x的一元一次方程,解之即可得出结论;
②设购进A种计算器y台,则购进C种计算器(50-y)台,根据总钱数=购进A种计算机的钱数+购进C种计算机的钱数即可列出关于y的一元一次方程,解之即可得出结论;
(2)当只购进B、C两种型号时,设购进B种计算器z台,则购进C种计算器(50-z)台,根据总钱数=购进B种计算机的钱数+购进C种计算机的钱数即可列出关于z的一元一次方程,解之即可得出z的值,从而得出此种进货方式不合理;当只购进A、B两种型号时,根据总利润=销售A种计算器的利润+销售B种计算器的利润即可算出选此方案时的利润;当只购进A、C两种型号时,根据总利润=销售A种计算器的利润+销售C种计算器的利润即可算出选此方案时的利润.二者比较后即可得出结论.
解答 (1)①设购进A种计算器x台,则购进B种计算器(50-x)台,
根据题意得:15x+21(50-x)=900,
解得:x=25,50-x=25.
答:购进A种计算器25台,B种计算器25台.
②设购进A种计算器y台,则购进C种计算器(50-y)台,
根据题意得:15y+25(50-y)=900,
解得:y=35,50-y=15.
答:购进A种计算器35台,B种计算器15台.
(2)当只购进B、C两种型号时,
设购进B种计算器z台,则购进C种计算器(50-z)台,
根据题意得:21z+25(50-z)=900,
解得:z=$\frac{175}{2}$(不合题意,舍去).
当只购进A、B两种型号时,
利润=25×5+25×8=325(元);
当只购进A、C两种型号时,
利润=35×5+15×12=421(元).
∵325<421,
∴选择购进A、C两种型号的计算器,销售时获利最多.
点评 本题考查了一元一次方程的应用,根据数量关系列出一元一次方程(或列式计算)是解题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 44厘米 | B. | 40厘米 | C. | 36厘米 | D. | 24厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元) | 180 | 260 | 280 | 300 |
| y(间) | 100 | 60 | 50 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
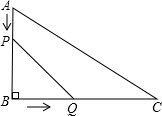 如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿着边AB向点B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以4cm/s的速度移动(不与点C重合).若P、Q两点同时移动t(s);
如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿着边AB向点B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿着边BC向点C以4cm/s的速度移动(不与点C重合).若P、Q两点同时移动t(s);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com