【题目】如图所示，A、B、C、D在同一直线上，AB＝CD，DE∥AF，若要使△ACF≌△DBE，则还需要补充一个条件：_____．
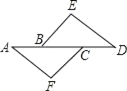
【答案】 AF＝DE或∠E＝∠F或BE∥CF
【解析】
本题要判定△ACF≌△DBE，由已知DE∥AF可得∠A=∠D，又有AC=BD，具备了一组角、一组边对应相等，然后根据全等三角形的判定定理，有针对性的添加条件．
解：添加AF=DE、∠E=∠F、BE∥CF、∠ACF=∠DBE后可分别根据SAS、AAS、ASA、ASA能判定△ACF≌△DBE．
故填AF=DE、∠E=∠F、BE∥CF、∠ACF=∠DBE等，答案不唯一．
考查三角形全等的判定方法；判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．添加时注意：AAA、SSA不能判定两个三角形全等，不能添加，根据已知结合图形及判定方法选择条件是正确解答本题的关健．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】为了传承优秀传统文化，我市组织了一次七年级1200名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了100名学生的成绩（满分50分），整理得到如下的统计图表：
组别 | 成绩分组 | 频数 | 频率 |
A | 35≤x＜38 | 3 | 0.03 |
B | 38≤x＜41 | a | 0.12 |
C | 41≤x＜44 | 20 | 0.20 |
D | 44≤x＜47 | 35 | 0.35 |
E | 47≤x≤50 | 30 | b |
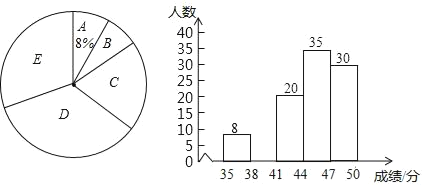
请根据所提供的信息解答下列问题：
（1）频率统计表中a＝ ，b＝ ；
（2）请补全频数分布直方图；
（3）在扇形统计图中D组的圆心角是 度；
（4）请根据抽样统计结果，估计该次大赛中成绩不低于41分的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一段抛物线：y＝－x(x－3)（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x 轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；
……
如此进行下去，直至得C13．
若P（1，m）在C1上，则m =_________．
若P（37，n）在第13段抛物线C13上，则n =_________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC。其中一定能判断这个四边形是平行四边形的条件共有
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】密码锁有三个转轮，每个转轮上有十个数字：0，1，2，…9．小黄同学是9月份中旬出生，用生日“月份+日期”设置密码：9××
小张同学要破解其密码：
（1）第一个转轮设置的数字是9，第二个转轮设置的数字可能是 ．
（2）请你帮小张同学列举出所有可能的密码，并求密码数能被3整除的概率；
（3）小张同学是6月份出生，根据（1）（2）的规律，请你推算用小张生日设置的密码的所有可能个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算
(1)(
)﹣2﹣(﹣2)0+(﹣0.2)2018×(﹣5)2018；
(2)用整式乘法公式计算：1012﹣1；
(3)(x2y+2x2y﹣y3)÷y﹣(y+2x)(2x﹣y)；
(4)先化简，再求值：(a﹣2b)2+(a﹣b)(a+b)﹣2(a﹣3b)(a﹣b)，其中，a＝1，b＝﹣2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理（解析）
提出问题：如图1，在四边形ABCD中，P是AD边上任意一点，△PBC与△ABC和△DBC的面积之间有什么关系？探究发现：为了解决这个问题，我们可以先从一些简单的、特殊的情形入手：
当AP＝
AD时(如图2)：
∵AP＝AD，△ABP和△ABD的高相等，
∴S△ABP＝S△ABD，
∵PD＝AD﹣AP＝AD，△CDP和△CDA的高相等
∴S△CDP＝S△CDA，
∴S△PBC＝S四边形ABCD﹣S△ABP﹣S△CDP＝S四边形ABCD﹣S△ABD﹣S△CDA，
＝S四边形ABCD﹣(S四边形ABCD﹣S△DBC)﹣(S四边形ABCD﹣S△ABC)＝S△DBC+S△ABC.
(1)当AP＝
AD时，探求S△PBC与S△ABC和S△DBC之间的关系式并证明；
(2)当AP＝
AD时，S△PBC与S△ABC和S△DBC之间的关系式为： ；
(3)一般地，当AP＝
AD(n表示正整数)时，探求S△PBC与S△ABC和S△DBC之间的关系为： ；
(4)当AP＝
AD(0≤≤1)时，S△PBC与S△ABC和S△DBC之间的关系式为： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2；（填“＞”或“＜”或“＝”）
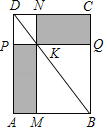
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
