
【题目】已知今年小明的年龄是x岁,小红的年龄比小明的2倍少4岁,小华的年龄比小红的 ![]() 还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含x的式子表示小刚的年龄,并计算当x=5时小刚的年龄.
还大1岁,小刚的年龄恰好为小明、小红、小华三个人年龄的和.试用含x的式子表示小刚的年龄,并计算当x=5时小刚的年龄.
【答案】解:
∵小红的年龄比小明的2倍少4岁,
∴小红的年龄为(2x﹣4)岁,
∵小华的年龄比小红的 ![]() 还大1岁,
还大1岁,
∴小华的年龄为[ ![]() (2x﹣4)+1]岁,
(2x﹣4)+1]岁,
∵小刚的年龄恰好为小明、小红、小华三个人年龄的和,
∴小刚的年龄为x+(2x﹣4)+ ![]() (2x﹣4)+1=x+2x﹣4+x﹣2+1=4x﹣5,
(2x﹣4)+1=x+2x﹣4+x﹣2+1=4x﹣5,
当x=5时,上式=4×5﹣5=15,
即当x=5时,小刚的年龄为15岁
【解析】根据题意可分别用x表示出小红、小华的年龄,由条件可表示出小刚的年龄,把x=5代入计算即可.
【考点精析】本题主要考查了代数式求值的相关知识点,需要掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知a,b,c在数轴上的位置如图所示,所对应的点分别为A,B,C. ![]()
(1)填空:A,B之间的距离为 , B,C之间的距离为 , A,C之间的距离为;
(2)化简:|a+b|﹣|c﹣b|+|b﹣a|;
(3)a、b、c在数轴上的位置如图所示,且c2=4,﹣b的倒数是它本身,a的绝对值的相反数是﹣2,求﹣a+2b﹣c﹣2(a﹣4c﹣b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题引入】
已知:如图BE、CF是ΔABC的中线,BE、CF相交于G。求证: ![]()
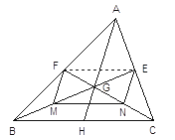
证明:连结EF
∵E、F分别是AC、AB的中点
∴EF∥BF且EF=![]() BC
BC
∴![]()
【思考解答】
(1)连结AG并延长AG交BC于H,点H是否为BC中点 (填“是”或“不是”)
(2)①如果M、N分别是GB、GC的中点,则四边形EFMN 是 四边形。
②当![]() 的值为 时,四边形EFMN 是矩形。
的值为 时,四边形EFMN 是矩形。
③当![]() 的值为 时,四边形EFMN 是菱形。
的值为 时,四边形EFMN 是菱形。
④如果AB=AC,且AB=10,BC=16,则四边形EFMN的面积![]() =_________
=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1cm的若干个正方形叠加行成的图形,其中第一个图形由1个正方形组成,周长为4cm,第二个图形由4个正方形组成,周长为10cm.第三个图形由9个正方形组成,周长为16cm,依次规律… 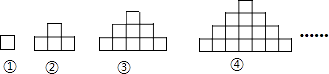
(1)第四个图形有个正方形组成,周长为cm.
(2)第n个图形有个正方形组成,周长为cm.
(3)若某图形的周长为58cm,计算该图形由多少个正方形叠加形成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A和点B的坐标分别为A(4,0)、B(0,2),将△ABO绕点P(2,2)顺时针旋转得到△OCD,点A、B和O的对应点分别为点O、C和D,
(1)画出△OCD,并写出点C和点D的坐标;
(2)连接AC,在直线AC的右侧取点M,使∠AMC=45°,
①若点M在x轴上,则点M的坐标为 ;
②若△ACM为直角三角形,求点M的坐标;
(3)若点N满足∠ANC>45°,请确定点N的位置(不要求说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
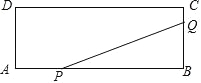
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(![]() ).
).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com