
【题目】一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为![]() .
.
(1)求口袋中白球的个数;
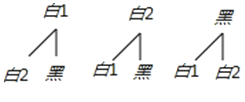
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
【答案】解:(1)∵一个口袋中有1个黑球和若干个白球,从中任意摸取一个球,摸得黑球的概率为![]() .
.
∴假设白球有x个,
∴![]() =
=![]() ,
,
∴x=2.
∴口袋中白球的个数为2个;
(2)∵先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.
∴两次都摸到白球的概率为:![]() .
.
【解析】(1)根据摸得黑球的概率为![]() , 假设出白球个数直接得出答案;
, 假设出白球个数直接得出答案;
(2)利用先随机从口袋中摸出一球,不放回,得出树状图即可.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


科目:初中数学 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x1 , x2(x1<x2)是方程(x﹣a)(x﹣b)=1(a<b)的两个根,则实数x1 , x2 , a,b的大小关系为( )
A.x1<x2<a<b
B.x1<a<x2<b
C.x1<a<b<x2
D.a<x1<b<x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC折叠,使B落在E处,AE交CD于点F,则下列结论中不一定成立的是( )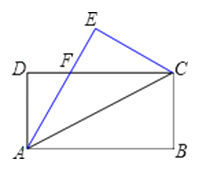
A.AD=CE
B.AF=CF
C.△ADF≌△CEF
D.∠DAF=∠CAF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从超市出发,向东走了![]() 千米到达小彬家,继续走
千米到达小彬家,继续走![]() 千米到达小颖家,然后向西走了
千米到达小颖家,然后向西走了![]() 千米到达小明家,最后回到超市.
千米到达小明家,最后回到超市.
![]()
![]() 以超市为原点,以向东的方向为正方向,用
以超市为原点,以向东的方向为正方向,用![]() 个单位长度表示
个单位长度表示![]() 千米,在数轴上表示出小明家,小彬家,小颖家的位置.
千米,在数轴上表示出小明家,小彬家,小颖家的位置.
![]() 小明家距小彬家多远?
小明家距小彬家多远?
![]() 若该货车每千米耗油
若该货车每千米耗油![]() 升,每升油
升,每升油![]() 元,那么这辆货车在行驶中一共花费多少油钱?
元,那么这辆货车在行驶中一共花费多少油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下内容,并解决所提出的问题:
![]() 我们知道:
我们知道:![]() ;
;![]() ;所以
;所以![]() .
.
![]() 用与
用与![]() 相同的方法可计算得
相同的方法可计算得![]() ;
;![]() .
.
![]() 归纳以上的学习过程,可猜测结论:
归纳以上的学习过程,可猜测结论:![]() ________.
________.
![]() 利用以上的结论计算以下各题:①
利用以上的结论计算以下各题:①![]() ________;②
________;②![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为﹣1,3,则下列结论正确的个数有( )
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com