
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①由抛物线开口向下a>0,抛物线和y轴的正半轴相交,c>0,-$\frac{b}{2a}$<0,b<0,所以abc<0;
②根据抛物线与x轴有一个交点,得到b2-4ac=0,于是得到b2=4ac;
③根据x=-1时,y=a+c-b=0,判断结论;
⑤根据x=-1时,函数y=a+b+c的值最小,得出当m≠-1时,有a-b+c>am2+bm+c,判断结论.
解答 解:∵开口向上,∴a>0,
∵抛物线和y轴的正半轴相交,∴c>0,
∵对称轴为x=-$\frac{b}{2a}$=-1,∴b=2a<0,
∴abc<0,故①正确;
∵抛物线与x轴有一个交点,
∴b2-4ac=0,
∴b2=4ac;故②正确;
∵当x=-1时,a-b+c=0,
∴a+c=b,故③错误;
∵当x=-1时,二次函数有最小值,所以当m≠-1时,有a-b+c<am2+bm+c,所以a<m(am+b)+b,故④正确.
故选C.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换的熟练运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;
(1)如图,木棒AB位于点光源P和地面CD之间,AB∥CD,若光源P到木棒AB的距离是1米,木棒AB到底面的距离也为1米,测得木棒AB的长度为2米,求木棒AB在地面的影长CD;| 光源P到木棒AB的距离 | 木棒AB在地面的影长 |
| 1米 | 4 |
| 2米 | 3 |
| 3米 | $\frac{8}{3}$ |
| …. | |
| 结论:平行于地面的线段长度一定,到地面的距离一定,则其上方的光源逐渐远离线段时,该线段在地面上的影长逐渐变小(填“变大”或“变小”). | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
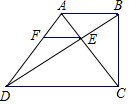 如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.
如图,在四边形ABCD中,AB∥CD,∠ABC=90°,CD=2AB,对角线AC与BD相交于点E,EF∥CD交AD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
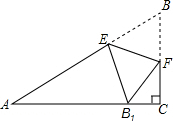 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com