
【题目】如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( ) 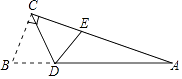
A.30°
B.40°
C.50°
D.70°
科目:初中数学 来源: 题型:
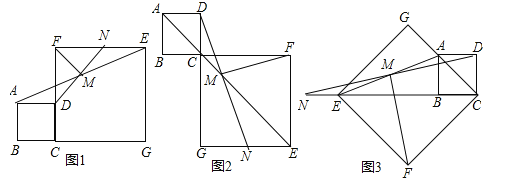
【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
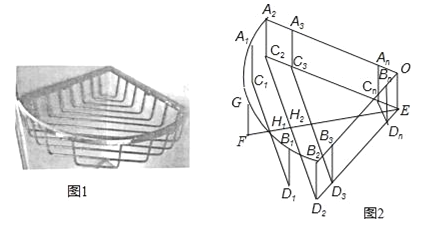
【题目】如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2,矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn,OEFG围成,其中A1、G、B1在![]() 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2,C1D1⊥EF于H1,FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
(1)求d的值;
(2)问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】与 ![]() 在平
在平![]() 面直角坐标系中的位置如图.
面直角坐标系中的位置如图.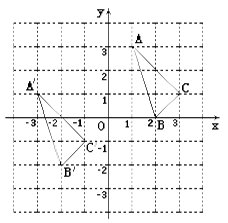
(1)分别写出下列各点的坐标:![]() ;
; ![]() ;
; ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:
经过怎样的平移得到:
.
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的
内的
对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论: ①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有( )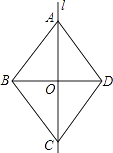
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.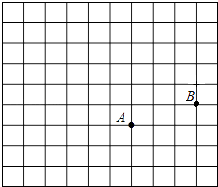
(1)建立适当的平面直角坐标系,使点A点B的坐标分别为(1,2)(4,3);
(2)点C的坐标为(3,6),在平面直角坐标系中找到点C的位置,连接AB、BC、CA,则∠ACB=°;
(3)将点A、B、C的横坐标都乘以﹣1,纵坐标不变,分别得到点A1、B1、C1 , 在图中找到点A1、B1、C1并顺次连接点A1、B1、C1 , 得到△A1B1C1 , 则这两个三角形关于对称.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com