
 如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$.
如图,在同一平面内,圆O和直线AB相切,P是圆O上一个定点,初始位置圆O和AB相切于点A(此时点P与点A重合),从A处开始圆O在直线AB上以每3分钟1圈的速度匀速向右无滑动地滚动,1分钟到达点E(圆O与AB相切于点E),此时,tan∠PAE的值为$\frac{9}{4π-3\sqrt{3}}$. 分析 如图所示,过点P作PC⊥AB,垂足为C,过点O作OD⊥PC,垂足为D.先求得∠POE=120°,从而可求得劣弧PE的弧长度即AE的长度,然后求得∠POD=30°,从而可求得PD和OD的长,然后证明四边形ODCE为矩形,接下来可求得AC和PC的长,从而可求得tan∠PAE的值.
解答 解:如图所示,过点P作PC⊥AB,垂足为C,过点O作OD⊥PC,垂足为D.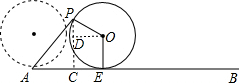
根据题意可知∠POE=$\frac{1}{3}×360°$=120°,AE=劣弧PE的弧长.
∴AE=2πR×$\frac{1}{3}$=$\frac{2πR}{3}$.
∵AB是圆O的切线,
∴∠OEC=90°.
∵PC⊥AB,OD⊥PC,
∴∠DCE=∠ODC=90°.
∴∠OEC=∠DCE=∠ODC=90°.
∴四边形ODCE为矩形.
∴DC=OE=R,OD=CE.
∵∠POD=30°,∠PDO=90°,
∴PD=$\frac{1}{2}PO=\frac{1}{2}R$,DO=$\frac{\sqrt{3}}{2}PO$=$\frac{\sqrt{3}}{2}R$.
∴PC=PD+DC=$\frac{3}{2}R$,AC=AE-EC=$\frac{2πR}{3}$-$\frac{\sqrt{3}R}{2}$.
∴tan∠PAE=$\frac{PC}{AC}$=$\frac{\frac{3}{2}R}{\frac{2πR}{3}-\frac{\sqrt{3}R}{2}}$=$\frac{\frac{3}{2}R}{\frac{4πR-3\sqrt{3}R}{6}}$=$\frac{9}{4π-3\sqrt{3}}$.
故答案为:$\frac{9}{4π-3\sqrt{3}}$.
点评 本题主要考查扇形的弧长公式、含30度直角三角形的性质、矩形的判定和性质,锐角三角函数的定义,明确AE等于劣弧PE的弧长是解题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
 一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?
一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com