
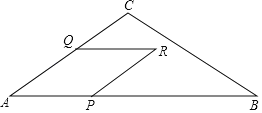
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌACЃНBCЃН5ЃЌABЃН8ЃЌЕуPдкABЩЯЃЌЕуQдкACЛђACЕФбгГЄЯпЩЯЃЌAQЃНAPЃЌвдAPЁЂAQЮЊСкБпзїСтаЮAPRQЃЌЩшAPЕФГЄЮЊxЃЌСтаЮAPRQгыЁїABCжигАВПЗжЭМаЮЕФУцЛ§ЮЊy(ЦНЗНЕЅЮЛ)ЃЌ
(1)ЧѓsinAЕФжЕ.
(2)ЕБxЮЊКЮжЕЪБЃЌЕуRТфдкBCЩЯ.
(3)ЕБСтаЮAPRQгыЁїABCжиЕўВПЗжЕФЭМаЮЮЊЫФБпаЮЪБЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪН.
(4)жБНгаДГіЕБxЮЊКЮжЕЪБЃЌОЙ§Ш§НЧаЮЖЅЕуЕФжБЯпЭЌЪБНЋСтаЮЁЂШ§НЧаЮЕФУцЛ§ЖўЕШЗж.
ЁОД№АИЁП(1)sinAЃН![]() ЃЛ(2)xЃН
ЃЛ(2)xЃН![]() ЃЛ(3)y=Љ
ЃЛ(3)y=Љ![]() x2+3x+8ЃЛ(4)ТњзуЬѕМўЕФxЕФжЕЮЊ
x2+3x+8ЃЛ(4)ТњзуЬѕМўЕФxЕФжЕЮЊ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
(1)ШчЭМ1жаЃЌзїCDЁЭABгкD.ИљОнЕШбќШ§НЧаЮЕФаджЪвдМАЙДЙЩЖЈРэЧѓГіCDМДПЩНтОіЮЪЬт.
(2)гЩQRЁЮBCЃЌПЩЕУ![]() ЃН
ЃН![]() ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬт.
ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬт.
(3)ЗжСНжжЧщаЮЃКЂйЕБ0ЃМxЁм![]() ЪБЃЌжиЕўВПЗжЪЧСтаЮAPRQ.ЂкШчЭМ3жаЃЌЕБ5ЁмxЃМ8ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPMCЃЌзїMHЁЭPBгкH.ЗжБ№ЧѓНтМДПЩ.
ЪБЃЌжиЕўВПЗжЪЧСтаЮAPRQ.ЂкШчЭМ3жаЃЌЕБ5ЁмxЃМ8ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPMCЃЌзїMHЁЭPBгкH.ЗжБ№ЧѓНтМДПЩ.
(4)ЗжСНжжЧщаЮЃКСЌНгARЃЌPQНЛгкЕуOЃЌЕБЕуOдкЁїABCЕФжаЯпBMЩЯЪБЃЌТњзуЬѕМў.ШчЭМ4жаЃЌзїOHЁЮABНЛACгкH.ШчЭМ5жаЃЌЕБЕуOТфдкжаЯпADЩЯЪБЃЌТњзуЬѕМў.ЗжБ№РћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬт.
НтЃК(1)ШчЭМ1жаЃЌзїCDЁЭABгкD.
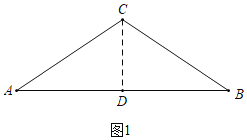
ЁпCAЃНCBЃН5ЃЌCDЁЭABЃЌ
ЁрADЃНDBЃН4ЃЌЁЯADCЃН90ЁуЃЌ
ЁрCDЃН![]() ЃН
ЃН![]() ЃН3.
ЃН3.
ЁрsinAЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
(2)ШчЭМ2жаЃЌЕБЕуRТфдкBCЩЯЪБЃЌ
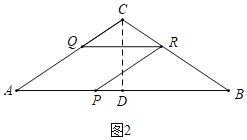
ЁпQRЁЮBCЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрxЃН![]() .
.
(3)ЂйЕБ0ЃМxЁм![]() ЪБЃЌжиЕўВПЗжЪЧСтаЮAPRQЃЌSЃНPAAQsinAЃНx
ЪБЃЌжиЕўВПЗжЪЧСтаЮAPRQЃЌSЃНPAAQsinAЃНx![]() xЃН
xЃН![]() x2.
x2.
ЂкШчЭМ3жаЃЌЕБ5ЁмxЃМ8ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮAPMCЃЌзїMHЁЭPBгкH.
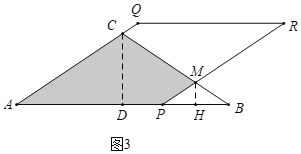
дкRtЁїMPHжаЃЌPHЃНBHЃН![]() ЃЌ
ЃЌ
MHЃНPHtanЁЯMPHЃН![]()
![]()
SЃНSЁїABCЉSЁїPBMЃН![]() ЁС8ЁС5Љ
ЁС8ЁС5Љ![]() (8Љx)
(8Љx)![]()
![]() ЃНЉ
ЃНЉ![]() x2+3x+8.
x2+3x+8.
(4)СЌНгARЃЌPQНЛгкЕуOЃЌЕБЕуOдкЁїABCЕФжаЯпBMЩЯЪБЃЌТњзуЬѕМў.ШчЭМ4жаЃЌзїOHЁЮABНЛACгкH.
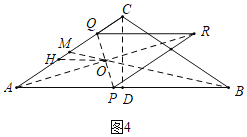
ЁпOQЃНOPЃЌOHЁЮPAЃЌ
ЁрAHЃНHQЃН![]() xЃЌOHЃН
xЃЌOHЃН![]() PAЃН
PAЃН![]() xЃЌ
xЃЌ
ЁпOHЁЮABЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр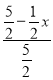 ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУxЃН![]() .
.
ШчЭМ5жаЃЌЕБЕуOТфдкжаЯпADЩЯЪБЃЌТњзуЬѕМў.
![]()
ЁпOHЁЮADЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФxЕФжЕЮЊ![]() Лђ
Лђ![]() .
.


 бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
бєЙтПЮЬУЭЌВНСЗЯАЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗжаМЧди:ЁАНёгаЩЯКЬШ§Бќ,вцЪЕСљЖЗ,ЕБЯТКЬЪЎБќ.ЯТКЬЮхБќ,вцЪЕвЛЖЗ,ЕБЩЯКЬЖўБќ.ЮЪЩЯЁЂЯТКЬЪЕвЛБќИїМИКЮ?ЁБЦфДѓвтЪЧ:НёгаЩЯЕШЕОзгШ§РІ,ШєДђГіРДЕФЙШзгдйМгСљЖЗ,дђЯрЕБгкЪЎРІЯТЕШЕОзгДђГіРДЕФЙШзг.гаЯТЕШЕОзгЮхРІ,ШєДђГіРДЕФЙШзгдйМгвЛЖЗ,дђЯрЕБгкСНРІЩЯЕШЕОзгДђчРДЕФЙШзг.ЮЪЩЯЕШЁЂЯТЕШЕОзгУПРІФмДђЖрЩйЖЗЙШзг?ЩшЩЯЕШЕОзгУПРІФмДђxЖЗЙШзг,ЯТЕШЕОзгУПРІФмДђyЖЗЙШзг,ИљОнЬтвт,ПЩСаЗНГЬзщЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
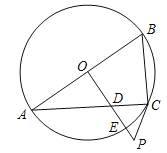
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌЙ§OЕузїOPЁЭABЃЌНЛЯвACгкЕуDЃЌНЛЁбOгкЕуEЃЌЧвЪЙЁЯPCA=ЁЯABCЃЎ
(1)ЧѓжЄЃКPCЪЧЁбOЕФЧаЯпЃЛ
(2)ШєЁЯP=60ЁуЃЌPC=2ЃЌЧѓPEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНmx+nЃЈmЁй0ЃЉЕФЭМЯѓгыyжсНЛгкЕуCЃЌгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAдкЕквЛЯѓЯоЃЌзнзјБъЮЊ4ЃЌЕуBдкЕкШ§ЯѓЯоЃЌBMЁЭxжсЃЌДЙзуЮЊЕуMЃЌBMЃНOMЃН2ЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌЕуAдкЕквЛЯѓЯоЃЌзнзјБъЮЊ4ЃЌЕуBдкЕкШ§ЯѓЯоЃЌBMЁЭxжсЃЌДЙзуЮЊЕуMЃЌBMЃНOMЃН2ЃЎ
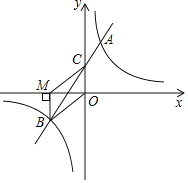
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉСЌНгOBЃЌMCЃЌЧѓЫФБпаЮMBOCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкФГвЛТЗЖЮЃЌЙцЖЈЦћГЕЯоЫйааЪЛЃЌНЛЭЈОЏВьдкДЫЯоЫйТЗЖЮЕФЕРТЗЩЯЩшжУСЫМрВтЧјЃЌЦфжаЕуCЁЂDЮЊМрВтЕуЃЌвбжЊЕуCЁЂDЁЂBдкЭЌвЛжБЯпЩЯЃЌЧвACЁЭBCЃЌCDЃН400УзЃЌtanЁЯADCЃН2ЃЌЁЯABCЃН35Ёу
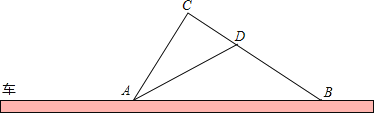
ЃЈ1ЃЉЧѓЕРТЗABЖЮЕФГЄЃЈНсЙћОЋШЗЕН1УзЃЉ
ЃЈ2ЃЉШчЙћЕРТЗABЕФЯоЫйЮЊ60ЧЇУз/ЪБЃЌвЛСОЦћГЕЭЈЙ§ABЖЮЕФЪБМфЮЊ90УыЃЌЧыФуХаЖЯИУГЕЪЧЗёЪЧГЌЫйЃЌВЂЫЕУїРэгЩЃЛВЮПМЪ§ОнЃКsin35ЁуЁж0.5736ЃЌcos35ЁуЁж0.8192ЃЌtan35ЁуЁж0.7002
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABCЕФШ§ИіЖЅЕуЗжБ№ЪЧAЃЈЃ3ЃЌ2ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
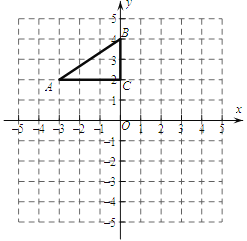
ЃЈ1ЃЉНЋЁїABCвдЕуCЮЊа§зЊжааФа§зЊ180ЁуЃЌЛГіа§зЊКѓЖдгІЕФЁї![]() CЃЛЦНвЦЁїABCЃЌШєAЕФЖдгІЕу
CЃЛЦНвЦЁїABCЃЌШєAЕФЖдгІЕу![]() ЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁї
ЕФзјБъЮЊЃЈ0ЃЌ4ЃЉЃЌЛГіЦНвЦКѓЖдгІЕФЁї![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєНЋЁї![]() CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁї
CШЦФГвЛЕуа§зЊПЩвдЕУЕНЁї![]() ЃЌЧыжБНгаДГіа§зЊжааФЕФзјБъЃЛ
ЃЌЧыжБНгаДГіа§зЊжааФЕФзјБъЃЛ
ЃЈ3ЃЉдк![]() жсЩЯгавЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
жсЩЯгавЛЕуPЃЌЪЙЕУPA+PBЕФжЕзюаЁЃЌЧыжБНгаДГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABOжаЃЌЁЯB=90 ЃЌOB=3,OA=5ЃЌвдAOЩЯвЛЕуPЮЊдВаФЃЌPOГЄЮЊАыОЖЕФдВЧЁКУгыABЯрЧагкЕуCЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉЃЎ
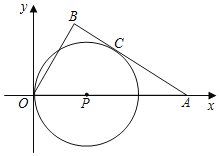
A.ЁбP ЕФАыОЖЮЊ![]()
B.ОЙ§AЃЌOЃЌBШ§ЕуЕФХзЮяЯпЕФКЏЪ§БэДяЪНЪЧ![]()
C.ЕуЃЈ3ЃЌ2ЃЉдкОЙ§AЃЌOЃЌBШ§ЕуЕФХзЮяЯпЩЯ
D.ОЙ§AЃЌOЃЌCШ§ЕуЕФХзЮяЯпЕФКЏЪ§БэДяЪНЪЧ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3ЃЌBC=4ЃЌOЮЊОиаЮABCDЕФжааФЃЌвдDЮЊдВаФ1ЮЊАыОЖзїЁбDЃЌPЮЊЁбDЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЁЂOPЃЌдђЁїAOPУцЛ§ЕФзюДѓжЕЮЊЃЈЁЁЁЁЃЉ

A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁїABCжаЃЌЕуDЃЌEЗжБ№дкБпABЃЌBCЩЯЃЌBABD=BCBE
ЃЈ1ЃЉЧѓжЄЃКЁїBDEЁзЁїBCAЃЛ
ЃЈ2ЃЉШчЙћAE=ACЃЌЧѓжЄЃКAC2=ADABЃЎ
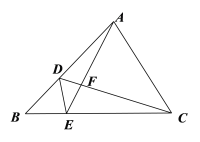
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com