
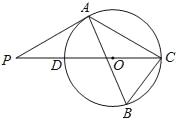
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)详见解析;(2)⊙O的半径为![]() .
.
【解析】
试题分析:(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,再由AP=AC得出∠P=30°,继而由∠OAP=∠AOC﹣∠P,可得出OA⊥PA,从而得出结论;
(2)过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=2![]() ,于是得到BE=
,于是得到BE=![]() BC=
BC=![]() ,CE=3,根据勾股定理得到AC=
,CE=3,根据勾股定理得到AC=![]() =5,于是得到AP=AC=5.解直角三角形即可得到结论.
=5,于是得到AP=AC=5.解直角三角形即可得到结论.
试题解析:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=∠AOC﹣∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线;
(2)解:过点C作CE⊥AB于点E.
在Rt△BCE中,∠B=60°,BC=2![]() ,
,
∴BE=![]() BC=
BC=![]() ,CE=3,
,CE=3,
∵AB=4+![]() ,
,
∴AE=AB﹣BE=4,
∴在Rt△ACE中,AC=![]() =5,
=5,
∴AP=AC=5.
∴在Rt△PAO中,OA=![]() ,
,
∴⊙O的半径为![]() .
.



 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
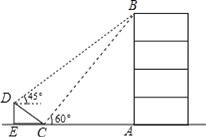
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
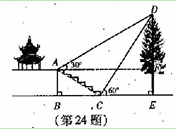
【题目】(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将1000元存入银行,定期一年,到期后他取出600元后,将剩下部分(包括利息)继续存入银行,定期还是一年,到期后全部取出,正好是550元,请问定期一年的利率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 于点
于点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
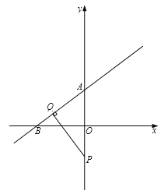
(1)求直线![]() 的解析式;
的解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)当![]() 在
在![]() 轴负半轴时,连接
轴负半轴时,连接![]() 、
、![]() ,分别取
,分别取![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,连接EF交PQ于点G,当OQ//BP时,求证:
,连接EF交PQ于点G,当OQ//BP时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=![]() (k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、B;过点Q分别作x轴、y轴的垂线,垂足为点C、D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )
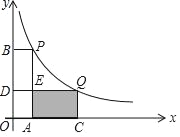
A. 增大 B. 减小
C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
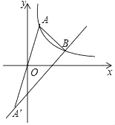
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1=![]() (x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(x>0)的图象上.点A与点A关于点O对称,一次函数y2=mx+n的图象经过点A.
(1)设a=2,点B(4,2)在函数y1,y2的图象上.
①分别求函数y1,y2的表达式;
②直接写出使y1>y2>0成立的x的范围.
(2)如图,设函数y1,y2的图象相交于点B,点B的横坐标为3a,△AA′B的面积为16,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
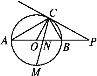
【题目】如图,AB是☉O的直径,点C在☉O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
(1)求证:PC是☉O的切线;
(2)点M是弧AB的中点,CM交AB于点N,若MN·MC=8,求☉O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B,E是半圆弧的三等分点,弧AB的长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A. 6![]() ﹣
﹣![]() B. 9
B. 9![]() ﹣
﹣![]() C.
C. ![]() ﹣
﹣![]() D. 6
D. 6![]() ﹣
﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com