
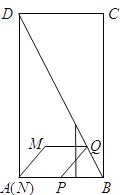
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 同时出发,点
同时出发,点![]() 沿折线
沿折线![]() 运动,在
运动,在![]() 上的速度是2
上的速度是2![]() /
/![]() ,在BC上的速度是
,在BC上的速度是![]()
![]() /
/![]() ;点
;点![]() 在
在![]() 上以2
上以2![]() /
/![]() 的速度向终点
的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .连结
.连结![]() ,以
,以![]() ,
,![]() 为邻边作平行四边形
为邻边作平行四边形![]() .设运动的时间为
.设运动的时间为![]() (s),平行四边形
(s),平行四边形![]() 与矩形
与矩形![]() 重叠部分的图形面积为
重叠部分的图形面积为![]()
![]()
(1)当![]() ⊥
⊥![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)直线![]() 将矩形
将矩形![]() 的面积分成1∶3两部分时,求
的面积分成1∶3两部分时,求![]() 的值.
的值.
【答案】(1)![]() s;(2)y=
s;(2)y=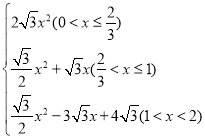 ;(3)x=
;(3)x=![]() 或
或![]() .
.
【解析】
(1)当PQ⊥AB时,BQ=2PB,由此构建方程即可解决问题;
(2)分三种情形:当0<x≤![]() 时,P在AB边上,M在矩形ABCD的内部或AD边上;当
时,P在AB边上,M在矩形ABCD的内部或AD边上;当![]() <x≤1时,P在AB边上,M在矩形ABCD的外部;当1<x<2时,P在BC边上,M在矩形ABCD的外部。分别求解即可解决问题;
<x≤1时,P在AB边上,M在矩形ABCD的外部;当1<x<2时,P在BC边上,M在矩形ABCD的外部。分别求解即可解决问题;
(3)分两种情形:当直线AM经过BC中点E时;当直线AM经过CD的中点E时。分别求解即可解决问题;
解:(1)当PQ⊥AB时,BQ=2PB,
∴2x=2(2-2x),
∴x=![]() s.
s.
故答案为![]() s.
s.
(2)①如图1中,当0<x≤![]() 时,P在AB边上,M在矩形ABCD的内部或AD边上,此时重叠部分是四边形PQMN.
时,P在AB边上,M在矩形ABCD的内部或AD边上,此时重叠部分是四边形PQMN.
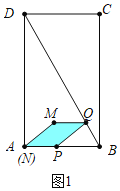
y=2x×![]() x=2
x=2![]() x2.
x2.
②如图2中,当![]() <x≤1时,P在AB边上,M在矩形ABCD的外部,此时重叠部分是四边形PQEN.
<x≤1时,P在AB边上,M在矩形ABCD的外部,此时重叠部分是四边形PQEN.
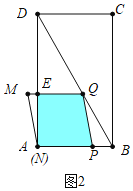
y=![]() (2-x+2x)×
(2-x+2x)×![]() x=
x=![]() x2+
x2+![]() x
x
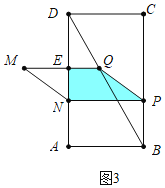
③如图3中,当1<x<2时,P在BC边上,M在矩形ABCD的外部,此时重叠部分是四边形PNEQ.
y=![]() (2-x+2)×[
(2-x+2)×[![]() x-2
x-2![]() (x-1)]=
(x-1)]=![]() x2-3
x2-3![]() x+4
x+4![]() ;
;
综上所述,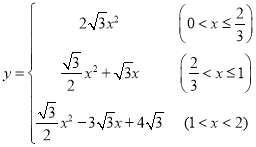 .
.
(3)①如图4中,当直线AM经过BC中点E时,满足条件.
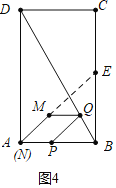
则有:tan∠EAB=tan∠QPB,
![]() ,
,
解得![]() .
.
②如图5中,当直线AM经过CD的中点E时,满足条件.
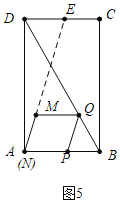
此时tan∠DEA=tan∠QPB,
![]() ,
,
解得![]() 。
。
综上所述,当![]() 或
或![]() 时,直线AM将矩形ABCD的面积分成1:3两部分.
时,直线AM将矩形ABCD的面积分成1:3两部分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
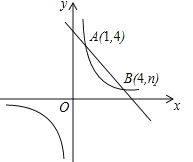
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是( )
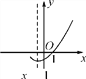
A. ①② B. ②③ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
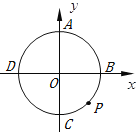
【题目】如图,半径为![]() 且坐标原点为圆心的圆交
且坐标原点为圆心的圆交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 、
、![]() 、
、![]() ,过圆上的一动点
,过圆上的一动点![]() (不与
(不与![]() 重合)作
重合)作![]() ,且
,且![]() (
(![]() 在
在![]()
![]() 右侧)
右侧)
(1)连结![]() ,当
,当![]() 时,则点
时,则点![]() 的横坐标是______.
的横坐标是______.
(2)连结![]() ,设线段
,设线段![]() 的长为
的长为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】举世瞩目的港珠澳大桥已于2018年10月24日正式通车,这座大桥是世界上最长的跨海大桥,被英国《卫报》誉为“新世界七大奇迹之一”当车辆经过这座大桥的收费站时,需从已开放的4个收费通道A、B、C、D中随机选择一个通过晶晶和贝贝两位同学的爸爸相约分别驾车经港珠澳大桥到香港旅行.
(1)晶晶的爸爸驾车通过收费站时,选择A通道通过的概率是多少?
(2)用画树状图或列表法求这两辆车经过此收费站时,选择不同通道通过的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
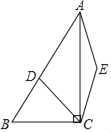
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=4,D是AB上一个动点,将点D绕点C顺时针旋转60°,得到点E,连接AE.若AE=![]() ,则BD=_____.
,则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边分别交CB、
绕点A顺时针旋转,它的两边分别交CB、![]() 或它们的延长线
或它们的延长线![]() 于点M、N,当
于点M、N,当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,则
,则

![]() 线段BM、DN和MN之间的数量关系是______;
线段BM、DN和MN之间的数量关系是______;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 时
时![]() 如图
如图![]() ,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
,线段BM、DN和MN之间有怎样的数量关系?写出猜想,并加以证明;
![]() 当
当![]() 绕点A旋转到
绕点A旋转到![]() 如图
如图![]() 的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
的位置时,线段BM、DN和MN之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com