
| A�� | �������M����������ȵ�ʵ��������ô����NҲ����������ȵ�ʵ���� | |
| B�� | ���6�Ƿ���M��һ��������ô$\frac{1}{6}$�Ƿ���N��һ���� | |
| C�� | �������M�ͷ���N��һ����ͬ�ĸ�����ô���������x=-1 | |
| D�� | �������M�������������죬��ô����N����������Ҳ���� |
���� �����б�ʽ������ɶ�A�����жϣ����ݷ��̸��Ķ����B�����жϣ�������������õģ�a-c��x2=a-c�����x=��1����ɶ�C�����жϣ����ݸ���ϵ���Ĺ�ϵ�ɶ�D�����жϣ�
��� �⣺A������M����������ȵ�ʵ���������=b2-4ac��0�����Է���NҲ����������ȵ�ʵ����������Aѡ��Ľ�����ȷ��
B����Ϊ6�Ƿ���M��һ��������36a+6b+c=0����$\frac{1}{36}$c+$\frac{1}{6}$b+a=0������$\frac{1}{6}$�Ƿ���N��һ����������Bѡ��Ľ�����ȷ��
C����Ϊ����M�ͷ���N��һ����ͬ�ĸ�����a-c��x2=a-c�����x=��1������Cѡ��Ľ��۴���
D������M�������������죬��$\frac{c}{a}$��0������$\frac{a}{c}$��0�����Է���N����������Ҳ���죬����Dѡ��Ľ�����ȷ��
��ѡC��
���� ���⿼���˸����б�ʽ��һԪ���η���ax2+bx+c=0��a��0���ĸ����=b2-4ac�����¹�ϵ��������0ʱ����������������ȵ�����ʵ����������=0ʱ��������������ȵ�����ʵ������������0ʱ��������ʵ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
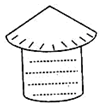 ��ͼ�����ֵĶ�����Բ���أ����Բ����Բ�뾶��Ϊ3m��ĸ�߳�Ϊ6m��Ϊ��ֹ��ˮ���������ֶ���������ձ�������ձ���г�����ÿƽ����10ԪǮ����ô������ձ����Ҫ�ķ�����108Ԫ��
��ͼ�����ֵĶ�����Բ���أ����Բ����Բ�뾶��Ϊ3m��ĸ�߳�Ϊ6m��Ϊ��ֹ��ˮ���������ֶ���������ձ�������ձ���г�����ÿƽ����10ԪǮ����ô������ձ����Ҫ�ķ�����108Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 50�� | B�� | 55�� | C�� | 65�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��-1�� | B�� | ��1��-1�� | C�� | ��-1��1�� | D�� | ��1��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��DC��8 | B�� | 3��DC��8 | C�� | 3��DC��5 | D�� | 3��DC��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{AC}{BC}$=$\frac{AB}{AC}$ | B�� | $\frac{AC}{AB}$=$\frac{AB}{BC}$ | C�� | $\frac{AB}{AC}$=$\frac{-1+\sqrt{5}}{2}$ | D�� | $\frac{AB}{BC}$=$\frac{-1+\sqrt{5}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | ��7 | C�� | -7 | D�� | 49 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
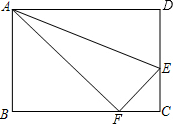 ��ͼ��С����һ�ų�����ֽƬABCD������ֽ����֪��ֽƬ��ABΪ4cm����BCΪ5cm����С���۵�ʱ������D����BC���ϵĵ�F�����ۺ�ΪAE������ʱFC�ij�����2cm��
��ͼ��С����һ�ų�����ֽƬABCD������ֽ����֪��ֽƬ��ABΪ4cm����BCΪ5cm����С���۵�ʱ������D����BC���ϵĵ�F�����ۺ�ΪAE������ʱFC�ij�����2cm���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com