
【题目】在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题:________(用题序号写).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】设p、q都是实数,且p<q.我们规定:满足不等式p≤x≤q的实数x的所有取值的全体叫做闭区间,表示为[p,q].对于一个函数,如果它的自变量x与函数值y满足:当p≤x≤q时,有p≤y≤q,我们就称此函数是闭区间[p,q]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由.
(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此一次函数的解析式;
(3)若实数c,d满足c<d,且d>2,当二次函数y=![]() x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
x2﹣2x是闭区间[c,d]上的“闭函数”时,求c,d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
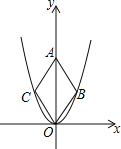
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com