
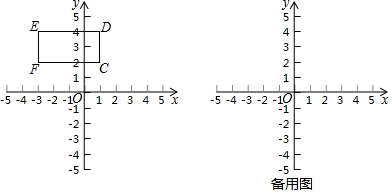
分析 (1)把抛物线解析式化为顶点式可求得其顶点坐标;
(2)由抛物线的对称性可知当开口向上时,离对称轴越近其函数值则越小,则可求得答案;
(3)由于抛物线的顶点确定,且开口向上,所以当抛物线开口越大时a的值越小,当抛物线开口越小时a的值越大,可知当抛物线过C时a有最小值,当抛物线过F时a有最大值,则可求得a的取值范围.
解答 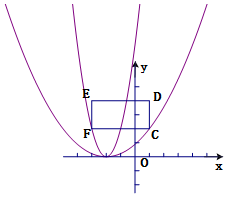 解:
解:
(1)∵y=a ( x 2+4x+4 )=a ( x+2 ) 2,
∴抛物线的顶点坐标为(-2,0);
(2)∵a>0,且对称轴为直线x=-2,
∴当函数图象上的点离对称轴越近时其函数值越小,
∵-4<m≤-3,0<n≤1,
∴A点离对称轴x=-2近,
∴y 1<y 2,
故答案为:<;
(3)∵y=a ( x+2 ) 2开口向上,且顶点为(-2,0),
∴当开口越大时a的值越小,当开口越小时a的值越大,
∴当抛物线过点C时a有最小值,当抛物线过点F时a有最大值
代入点C(1,2),得a=$\frac{2}{9}$,
代入点F(-3,2),得a=2,
∴$\frac{2}{9}$<a<2.
点评 本题为二次函数的综合应用,涉及二次函数的性质、二次函数的开口大小、二次函数的比较大小及数形结合思想等知识.在(1)中把二次函数解析式化为顶点式是解题的关键,在(2)中掌握抛物线上的点离对称轴的距离的远近与函数值的大小关系是解题的关键,在(3)中掌握抛物线的开口大小与二次项系数的关系是解题的关键.本题考查知识点不多,但综合性很强,难度适中.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:选择题
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 10 | |
| a | |
| 21 |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |a+b|的值一定是正数 | B. | a2+1的值一定是正数 | ||
| C. | 当a<b时,a2<b2 | D. | 当a>b时,|a|>|b| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
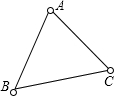 如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )
如图,兔子的三个洞口A、B、C构成△ABC,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在( )| A. | 三条边的垂直平分线的交点 | B. | 三个角的角平分线的交点 | ||
| C. | 三角形三条高的交点 | D. | 三角形三条中线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为lm/s,小华走的时间是( )
如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为lm/s,小华走的时间是( )| A. | 13 | B. | 8 | C. | 6 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com