
Čōx1”¢x2ŹĒ¹ŲÓŚŅ»ŌŖ¶ž“Ī·½³Ģax2£«bx£«c(a”Ł0)µÄĮ½øöøł£¬Ōņ·½³ĢµÄĮ½øöøłx1”¢x2ŗĶĻµŹża”¢b”¢cÓŠČēĻĀ¹ŲĻµ£ŗx1£«x2£½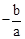 £¬x1•x2£½
£¬x1•x2£½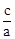 £®°ŃĖü³ĘĪŖŅ»ŌŖ¶ž“Ī·½³ĢøłÓėĻµŹż¹ŲĻµ¶ØĄķ£®Čē¹ūÉ趞“ĪŗÆŹży£½ax2£«bx£«c(a”Ł0)µÄĶ¼ĻóÓėxÖįµÄĮ½øö½»µćĪŖA(x1£¬0)£¬B(x2£¬0)£®ĄūÓĆøłÓėĻµŹż¹ŲĻµ¶ØĄķæÉŅŌµĆµ½A”¢BĮ¬øö½»µć¼äµÄ¾ąĄėĪŖ£ŗAB£½|x1£x2|£½
£®°ŃĖü³ĘĪŖŅ»ŌŖ¶ž“Ī·½³ĢøłÓėĻµŹż¹ŲĻµ¶ØĄķ£®Čē¹ūÉ趞“ĪŗÆŹży£½ax2£«bx£«c(a”Ł0)µÄĶ¼ĻóÓėxÖįµÄĮ½øö½»µćĪŖA(x1£¬0)£¬B(x2£¬0)£®ĄūÓĆøłÓėĻµŹż¹ŲĻµ¶ØĄķæÉŅŌµĆµ½A”¢BĮ¬øö½»µć¼äµÄ¾ąĄėĪŖ£ŗAB£½|x1£x2|£½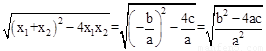
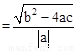 ӣ
ӣ
²Īæ¼ŅŌÉĻ¶ØĄķŗĶ½įĀŪ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
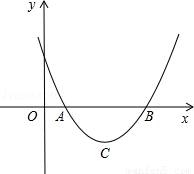
É趞“ĪŗÆŹży£½ax2£«bx£«c(a£¾0)µÄĶ¼ĻóÓėxÖįµÄĮ½øö½»µćA(x1£¬0)£¬B(x2£¬0)£¬Å×ĪļĻߵĶ„µćĪŖC£¬ĻŌČ»”÷ABCĪŖµČŃüČż½ĒŠĪ£®
(1)µ±”÷ABCĪŖÖ±½ĒČż½ĒŠĪŹ±£¬Ēób2£4acµÄÖµ£»
(2)µ±”÷ABCĪŖµČ±ßČż½ĒŠĪŹ±£¬Ēób2£4acµÄÖµ£®
£Ø1£©4£Ø2£©12
”¾½āĪö”æ½ā£ŗ£Ø1£©µ±”÷ABCĪŖÖ±½ĒČż½ĒŠĪŹ±£¬
¹żC×÷CE”ĶABÓŚE£¬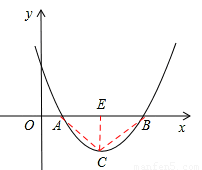
ŌņAB£½2CE”£
”ßÅ×ĪļĻßÓėxÖįÓŠĮ½øö½»µć£¬”÷£½b2£4ac£¾0£¬
Ōņ|b2£4ac|£½b2£4ac”£
”ßa£¾0£¬”ąAB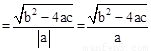 ”£
ӣ
ÓÖ”ßCE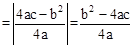 £¬”ą
£¬”ą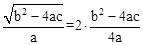 ”£
ӣ
”ą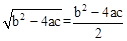 £¬¼“
£¬¼“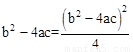 ”£
ӣ
”ßb2£4ac£¾0£¬”ąb2£4ac£½4”£
£Ø2£©µ±”÷ABCĪŖµČ±ßČż½ĒŠĪŹ±£¬ÓÉ(1)æÉÖŖCE£½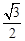 AB£¬
AB£¬
”ą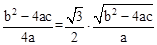 ”£
ӣ
”ßb2£4ac£¾0£¬”ąb2£4ac£½12”£
£Ø1£©µ±”÷ABCĪŖÖ±½ĒČż½ĒŠĪŹ±£¬ÓÉÓŚAC£½BC£¬ĖłŅŌ”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬¹żC×÷CE”ĶABÓŚE£¬ŌņAB£½2CE£®øł¾Ż±¾Ģā¶ØĄķŗĶ½įĀŪ£¬µĆµ½AB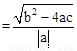 £¬øł¾Ż¶„µć×ų±ź¹«Ź½£¬µĆµ½CE
£¬øł¾Ż¶„µć×ų±ź¹«Ź½£¬µĆµ½CE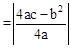 £¬ĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉĒó³öb2£4acµÄÖµ”£
£¬ĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉĒó³öb2£4acµÄÖµ”£
£Ø2£©µ±”÷ABCĪŖµČ±ßČż½ĒŠĪŹ±£¬½āÖ±½Ē”÷ACE£¬µĆCE£½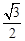 AB£¬¾Ż“ĖĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉĒó³öb2£4acµÄÖµ”£
AB£¬¾Ż“ĖĮŠ³ö·½³Ģ£¬½ā·½³Ģ¼“æÉĒó³öb2£4acµÄÖµ”£



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| b |
| a |
| c |
| a |
| 3 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŌĶĮĄķ½ā
| 4 |
| 3 |
| 10 |
| 3 |
| 8 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| b |
| a |
| b |
| a |
| c |
| a |
| c |
| a |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2010Äź±±¾©ŹŠ“óŠĖĒųÖŠæ¼ŹżŃ§Ņ»Ä£ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
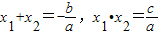 £®ĪŅĆĒ°ŃĖüĆĒ³ĘĪŖøłÓėĻµŹż¹ŲĻµ¶ØĄķ£®
£®ĪŅĆĒ°ŃĖüĆĒ³ĘĪŖøłÓėĻµŹż¹ŲĻµ¶ØĄķ£®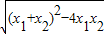 =
=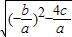 =
=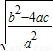 =
=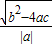
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ2012-2013ѧğø£½ØŹ”ÕÄÖŻŹŠĘ½ŗĶĻŲ¾ÅÄź¼¶£ØÉĻ£©ĘŚÖŠŹżŃ§ŹŌ¾ķ£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
 £®
£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com