练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在中，AC为对角线，BE^AC，DF^AC，E，F为垂足，求证：BE=DF。

     

    答案：
    解析：

    		证明：由平行四边形ABCD，可得AD=BC，AD平行CB，∴ ÐDAF=ÐBCA。由BE^AC，DF⊥AC，可推得：DADF≌DCBE，∴ BE=DF。

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    本题分为A、B 两类题，你可从A、B 两类题中任选一题解答即可
    （A类）：如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．
    （1）求四边形AQMP的周长；
    （2）写出图中的两对相似三角形（不需证明）；
    （3）M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由．
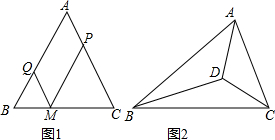    （B类）：有人这样证明三角形内角和是180°，如图，D是△ABC内一点，连接AD、BD、CD，他们将△ABC分成了三个小的三角形．因此有：三个小三角形的内角和的和比△ABC的内角和多360°，如果设三角形内角精英家教网和是x，则有：x+x+x=x+360°，易解得x=180°，你认为这个证明正确吗？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    1、如图，在?ABCD中，O为对角线AC、BD的交点，则图中共有相等的角（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在⊙O中，弦AC、BD相交于点P，已知弧AB、弧CD所对的圆心角的度数分别为65°和45°，则∠APB=
    55
    55
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

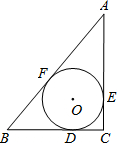    如图：在Rt△ABC中，∠C=Rt∠，⊙O是Rt△ABC的内切圆，切点分别是D、E、F，若三角形三边长分别记为BC=a，AC=b，AB=c，内切圆半径记为r，现有小明和小华对半径进行计算，小明计算结果为r=
    a+b-c
    2
    ，小华计算结果为r′=
    ab
    a+b+c
    ，由此两人产生争议．请问这两个答案是否都正确，如正确请结合图形说明理由，如不正确也请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•广阳区一模）九年级数学兴趣小组近期开展了对运动型问题的探究．小明同学提供了一个这样的背景：如图，在?ABCD中，AB=AC=10cm，sin∠ACB=
    45
    ，动点O从A出发以1cm/s的速度沿AC方向向点C匀速运动，同时线段EF从与线段CB重合的位置出发以1cm/s的速度沿BA方向向点C匀速运动．在运动过程中，EF交AC于点G，连接OE、OF．设运动时间为ts（0＜t＜10），请你解决以下问题：
    （1）当t为何值时，点O与点G重合？
    （2）当点O与点G不重合时，判断△OEF的形状，并说明理由．             
    （3）当0＜t＜5时，
        ①在上述运动过程中，五边形BCEOF的面积是否为定值？如果是，求出五边形BCEOF的面积；如果不是，请说明理由．
        ②△EOG的面积是否存在最大值？若存在，请求出最大值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案