
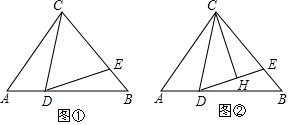
分析 (1)先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE;
(2)先根据条件得出∠DCB=∠CDE,进而得到CE=DE,再在DE上取点F,使得FD=BE,进而判定△CDF≌△DBE(SAS),得出CF=DE=CE,再根据CH⊥EF,运用三线合一即可得到FH=HE,最后得出DE-BE=DE-DF=EF=2HE=2.
解答  解:(1)∵AC=BC,∠CDE=∠A,
解:(1)∵AC=BC,∠CDE=∠A,
∴∠A=∠B=∠CDE,
∴∠ACD=∠BDE,
又∵BC=BD,
∴BD=AC,
在△ADC和△BED中,
$\left\{\begin{array}{l}{∠ACD=∠BDE}\\{AC=BD}\\{∠A=∠B}\end{array}\right.$,
∴△ADC≌△BED(ASA),
∴CD=DE;
(2)∵CD=BD,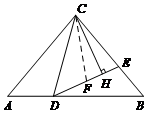
∴∠B=∠DCB,
又∵∠CDE=∠B,
∴∠DCB=∠CDE,
∴CE=DE,
如图,在DE上取点F,使得FD=BE,
在△CDF和△DBE中,
$\left\{\begin{array}{l}{DF=BE}\\{∠CDE=∠B}\\{CD=BD}\end{array}\right.$,
∴△CDF≌△DBE(SAS),
∴CF=DE=CE,
又∵CH⊥EF,
∴FH=HE,
∴DE-BE=DE-DF=EF=2HE=2.
点评 本题主要考查了全等三角形的判定与性质,以及等腰三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及等腰三角形,运用三线合一进行推理计算.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
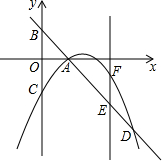 如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.
如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
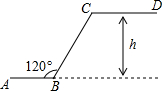 如图是某商场一楼与二楼之间手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=120°,BC的长是8m,则乘电梯从点B到点C上升的高度h是4$\sqrt{3}$m.
如图是某商场一楼与二楼之间手扶电梯示意图,其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=120°,BC的长是8m,则乘电梯从点B到点C上升的高度h是4$\sqrt{3}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
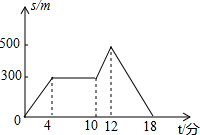 星期天晚饭后,小红从家里出发去散步,下图描述了她散步过程中离家的距离s(米)与散步所用的时间t(分)之间的关系,依据图象,下面描述符合小红散步情景的是( )
星期天晚饭后,小红从家里出发去散步,下图描述了她散步过程中离家的距离s(米)与散步所用的时间t(分)之间的关系,依据图象,下面描述符合小红散步情景的是( )| A. | 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 | |
| B. | 从家里出发,一直散步(没有停留),然后回家了 | |
| C. | 从家里出发,散了一会儿步,就找同学去了,18分钟后才开始返回 | |
| D. | 从家出发,到了一个公共阅报栏,看了一会报,继续向前走了一段后,然后回家了 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com