
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出
的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出![]() 在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数
在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数![]() 的图象与性质.
的图象与性质.

(1)该函数自变量x的取值范围_______________;
(2)通过分析解析式画出部分函数图象,如图2所示.请沿此思路在图2中完善函数图象的草图并标出此函数图象与y轴的交点A;(画出网格区域内的部分即可)
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() 有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
【答案】(1)x≥0且x≠1;(2)详见解析;(3)当x>1时,y随x的增大而减小(答案不唯一);(4)a≥1.
【解析】
(1)根据题意:x≥0,且≠1;(2)由x的取之范围可知,所以要画的图象是0≤x<1的部分;(3)观察图像,数形结合求解;(4)设y1=![]() ,y2=a(x-1),由关于x的方程
,y2=a(x-1),由关于x的方程![]() 有两个不相等的实数根可得两图象有两个交点,将特殊点A代入可得a=1,绕着(1,0)旋转y2图象可得范围.
有两个不相等的实数根可得两图象有两个交点,将特殊点A代入可得a=1,绕着(1,0)旋转y2图象可得范围.
解:(1)由![]() 可得:x≥0且
可得:x≥0且![]()
∴x≥0且x≠1
故答案为:x≥0且x≠1
(2)如图:

(3)有图可得:当x>1时,y随着x的增大而减小
故答案为:当x>1时,y随着x的增大而减小(答案不唯一)
(4)设y1=![]() ,y2=a(x-1)
,y2=a(x-1)
∴y2过定点(1,0)
∵关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根
∴y1的图象与y2的图象有两个交点.
若交点为A(0,-1),则a=1,
∴由图象可得a≥1
故答案为:a≥1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上,量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,![]() ≈1.73)
≈1.73)
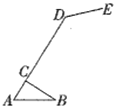
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某路灯灯架示意图,其中点A表示电灯,AB和BC为灯架,l表示地面,已知AB=2m,BC=5.7m,∠ABC=110°,BC⊥l于点C,求电灯A与地面l的距离.(结果精确到0.1m.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
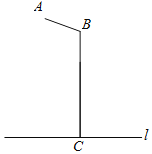
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学兴趣小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边是由周长为30米的篱笆围成.如图所示,已知墙长为20米,设这个苗圃园垂直于墙的一边长为x米
(1)若苗圃园的面积为108m2,求x的值,
(2)苗圃园的面积能达到120m2吗?若能,求出x;若不能,说明理由.
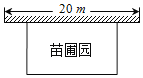
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.
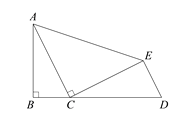
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于点A(﹣2,0),点B(1,0),交y轴于点C(0,2).

(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上有一点N,过点N作y轴的平行线,交直线AC于点F,设点N的横坐标为n,线段NF的长为l,求l关于n的函数关系式;
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.
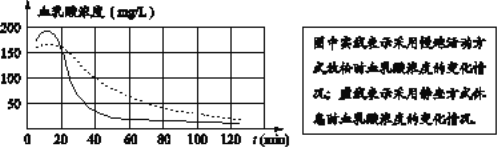
下列叙述正确的是
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后最高血乳酸浓度大约为350mg/L
C. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
D. 采用慢跑活动方式放松时,运动员必须慢跑80min后才能基本消除疲劳
查看答案和解析>>
科目:初中数学 来源: 题型:
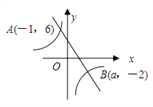
【题目】(8分)如图,一次函数y1=kx+b(k≠0)和反比例函数y2=![]() (m≠0)的图像交于点A(-1,6)、B(a,-2).
(m≠0)的图像交于点A(-1,6)、B(a,-2).
(1)求一次函数与反比例函数的解析式;
(2)根据图像直接写出y1>y2时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com