
分析 (1)将11分解为1+10、2+9、3+8、4+7、5+6,根据1×10<2×9<3×8<4×7<5×6即可求出F(11)的值;
(2)找出小于200且各位数字之和再加上1为一个完全平方数的数,再根据“多余数”的定义找出其中的最大数,重复(1)的操作,即可找出所有“多余数”中F(t)的最大值.
解答 解:(1)11可以分解成1+10、2+9、3+8、4+7、5+6,
∵1×10<2×9<3×8<4×7<5×6,
∴F(11)=5×6=30.
(2)小于200且各位数字之和再加上1为一个完全平方数的数有:195、186、177、170、168、161、159、152、143、134、125、120、116、111、107、102,
其中最大的“多余数”为170,
170可以分为1+169、2+168、…、84+86、85+85,
∵1×169<2×168<…<84×86<85×85,
∴F(170)=85×85=7225,
∴所有“多余数”中F(t)的最大值为7225.
点评 本题考查了因式分解的应用以及有理数的计算,解题的关键:(1)熟读题意,理解何为最佳分解;(2)找出符合题意得最大三位数.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
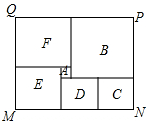 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
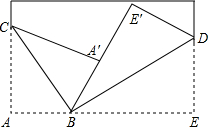 如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.
如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com