
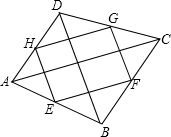
 ���ǰ�������������һ���ı��θ����е����õ��ı��ν����е��ı��Σ���ͼ��E��F��G��H�ֱ����ı���ABCD���ߵ��е㣬��֤�е��ı���EFGH��ƽ���ı��Σ�������Ƕ��ı���ABCD�ĶԽ���AC��BD����һ�������������ʹ�е��ı���EFGH��Ϊ�����ƽ���ı��Σ����㾭��̽����ش��������⣿
���ǰ�������������һ���ı��θ����е����õ��ı��ν����е��ı��Σ���ͼ��E��F��G��H�ֱ����ı���ABCD���ߵ��е㣬��֤�е��ı���EFGH��ƽ���ı��Σ�������Ƕ��ı���ABCD�ĶԽ���AC��BD����һ�������������ʹ�е��ı���EFGH��Ϊ�����ƽ���ı��Σ����㾭��̽����ش��������⣿���� ��1��֤��GH�ǡ�ACD����λ�ߣ��ó�GH��AC��GH=$\frac{1}{2}$AC��ͬ����EF��AC��EF=$\frac{1}{2}$AC��GF��BD��GF=$\frac{1}{2}$BD���ó�GH��EF��GH=EF��֤���ı���EFGH��ƽ���ı��Σ���֤��EF=GF�����ɵó����ۣ�
��ͬ�ٵã��ı���EFGH��ƽ���ı��Σ���AC��BD��֤����HGF=90�㣬�ó��ı���EFGHΪ���Σ�
��2����AC=BD�ó��ı���EFGHΪ���Σ���AC��BD�ó��ı���EFGHΪ���Σ����ɵó��ı���EFGHΪ�����Σ�
��� ��1���⣺�ٵ�AC=BDʱ���ı���EFGHΪ���Σ��������£�
��G��H�ֱ����ı���CD��AD���е㣬
��GH�ǡ�ACD����λ�ߣ�
��GH��AC��GH=$\frac{1}{2}$AC��
ͬ����EF��AC��EF=$\frac{1}{2}$AC��GF��BD��GF=$\frac{1}{2}$BD��
��GH��EF��GH=EF��
���ı���EFGH��ƽ���ı��Σ�
�֡�AC=BD��
��EF=GF��
���ı���EFGH�����Σ�
�ʴ�Ϊ��AC=BD��
�ڵ�AC��BDʱ���ı���EFGHΪ���Σ��������£�
ͬ�ٵã��ı���EFGH��ƽ���ı��Σ�
��AC��BD��GH��AC��
��GH��BD��
��GF��BD��
��GH��GF��
���HGF=90�㣬
���ı���EFGHΪ���Σ�
�ʴ�Ϊ��AC��BD��
��2���⣺��AC=BD��AC��BDʱ���ı���EFGHΪ�����Σ��������£�
��AC=BDʱ���ɢٵã��ı���EFGHΪ���Σ�
��AC��BDʱ���ɢڵã��ı���EFGHΪ���Σ�
���ı���EFGHΪ�����Σ�
���� ���⿼�����е��ı��Ρ�ƽ���ı��ε��ж������ε��ж������ε��ж��Լ������ε��ж�����������������������λ�߶��������ܽ���������֤�ǽ������Ĺؼ���


 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
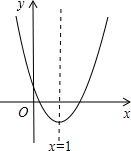 ��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���Գ�����ֱ��x=1�����н��ۣ���abc��0����2a+b=0����b2-4ac��0����4a+2b+c��0��������ȷ���ǣ�������
��֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���Գ�����ֱ��x=1�����н��ۣ���abc��0����2a+b=0����b2-4ac��0����4a+2b+c��0��������ȷ���ǣ�������| A�� | �٢� | B�� | �� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����D��x���ཻ��A��-2��0����B��-8��0������y��������C����Բ��D������Ϊ��-5��4����
��ͼ����D��x���ཻ��A��-2��0����B��-8��0������y��������C����Բ��D������Ϊ��-5��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
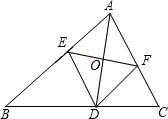 ��ͼ���ڡ�ABC�У�AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AC��DF��AB��EF��AD�ڵ�O������DO�ǡ�DEF�Ľ�ƽ��������˵�����ɣ�
��ͼ���ڡ�ABC�У�AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AC��DF��AB��EF��AD�ڵ�O������DO�ǡ�DEF�Ľ�ƽ��������˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
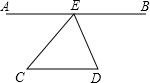 ��ͼ����֪��A��E��B��һͬ��ֱ���ϣ����CED=x����C+��D=y��
��ͼ����֪��A��E��B��һͬ��ֱ���ϣ����CED=x����C+��D=y���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x}{y}=\frac{3}{5}$ | B�� | $\frac{3+x}{x}=\frac{5+y}{y}$ | C�� | $\frac{x}{y}=\frac{5}{3}$ | D�� | $\frac{x-3}{3}=\frac{y-5}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2x-y��2=4x2+y2-2xy | B�� | ��a2+2b��2=a2+4a2b+4b2 | ||
| C�� | ��a-b��2=a2-b2 | D�� | ��$\frac{1}{2}$x+3��2=$\frac{1}{4}$x2+3x+9 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com