
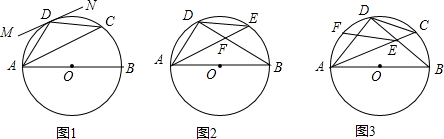
分析 (1)根据MN是⊙O的切线,得到∠ODM=90°,根据平行线的性质得到∠AKD=90°,由垂径定理得到AK=CK,根据等腰三角形的性质得到∠DAC=∠DCA等量代换即可得到结论;
(2)根据等边三角形的性质得到∠DOC=60°,由平角的定义得到∠AOD+∠BOC=120°,得到∠B+∠BAC=60°,于是得到结论;
(3)由AB是⊙O的直径,得到∠ACB=90°,解直角三角形得到CE=$\frac{1}{2}$BE,等量代换得到CE=$\frac{1}{2}$DE,根据勾股定理解方程求得CE=$\sqrt{7}$,ED=2$\sqrt{7}$,BD=4$\sqrt{7}$,推出四边形OGDE是矩形,根据矩形的性质得到∠FOE=90°,然后根据勾股定理即可得到结论.
解答 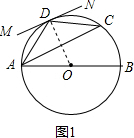 (1)证明:连接OD,交AC于点K,
(1)证明:连接OD,交AC于点K,
∵MN是⊙O的切线,
∴∠ODM=90°,
∵MN∥AC,
∴∠AKD=180°-∠ODM,
∴∠AKD=90°,
即OK⊥AC,
∴AK=CK,
∴AD=CD,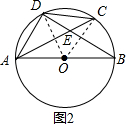
∴AD=CD,
∴∠DAC=∠DCA
∵MN∥AC,
∴∠ADM=∠DAC,∠CDN=∠DCA,
∴∠ADM=∠CDN;
(2)证明:连接OD,OC,
∵CD=OA,∴CD=OD=OC,
∴∠DOC=60°,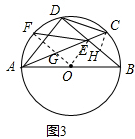
∴∠AOD+∠BOC=120°,
∵∠AOD=2∠B,∠BOC=2∠BAC,
∴2∠B+2∠BAC=120°,
∴∠B+∠BAC=60°,
∵∠BEC=∠B+∠BAC,
∴∠BEC=60°;
(3)解:连接OE,OF,OF交AD于点G,
∵AB是⊙O的直径,
∴∠ACB=90°,
由(2)知∠BEC=60°,
∴在Rt△BCE中,CE=cos60°BE,
∴CE=$\frac{1}{2}$BE,
∵BE=DE,
∴CE=$\frac{1}{2}$DE,
过点C作CH⊥BD于点H,
在Rt△CHE中,EH=ECcos60°=$\frac{1}{2}$EC,CH=EHtan60°=$\sqrt{3}$EH,
设EH=x,则CE=2x,CH=$\sqrt{3}$x,DE=4x,
在Rt△CHD中,
由勾股定理得CH2+DH2=CD2,即($\sqrt{3}$x)2+(4x+x)2=72,
解得x=±$\frac{\sqrt{7}}{2}$(负值舍去)
∴CE=$\sqrt{7}$,ED=2$\sqrt{7}$,BD=4$\sqrt{7}$,
∵CD=OA,
∴OB=7,
∵E是BD中点,
∴∠OED=90°,
在Rt△OEB中,OE=$\sqrt{O{B}^{2}-B{E}^{2}}$=$\sqrt{21}$,
∵F是AD中点,
∴∠OGD=90°,
∵AB是直径,
∴∠ADB=90°,
∴四边形OGDE是矩形,
∴∠FOE=90°,
在Rt△OEF中,EF=$\sqrt{O{E}^{2}+O{F}^{2}}$=$\sqrt{70}$.
点评 本题考查了切线的性质,平行线的性质,圆周角定理,勾股定理,矩形的判定和性质,解直角三角形,垂径定理,正确的理解题意,识别图形是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
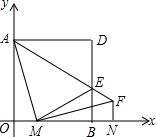 在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).
在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
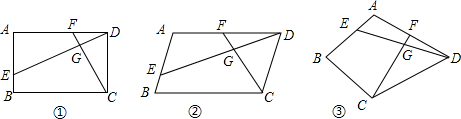 已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
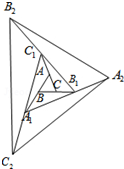 如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com