
分析 (1)利用配方法得到(x-2)2=5,然后利用直接开平方法解方程;
(2)利用求根公式法解方程.
解答 解:(1)x2-4x=1,
x2-4x+4=5,
(x-2)2=5,
x-2=±$\sqrt{5}$,
所以x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)△=32-4×2×(-1)=17,
x=$\frac{-3±\sqrt{17}}{2×2}$
所以x1=$\frac{-3+\sqrt{17}}{4}$,x2=$\frac{-3-\sqrt{17}}{4}$.
点评 本题考查了解一元二次方程-公式法:把x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$(b2-4ac≥0)叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式,用求根公式解一元二次方程的方法是公式法.也考查了配方法解一元二次方程.


科目:初中数学 来源: 题型:选择题
 如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、
如图,AB是半圆O的直径,C、D、E是半圆的四等分点,CH⊥AB于H,连接BD、| A. | ①②③ | B. | 只有①② | C. | 只有①③ | D. | 只有③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
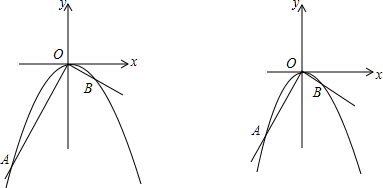
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA,若抛物线y=-x2-2x+c经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )
如图,△ABC的三个顶点都在方格纸的格点上,则sinA=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com