
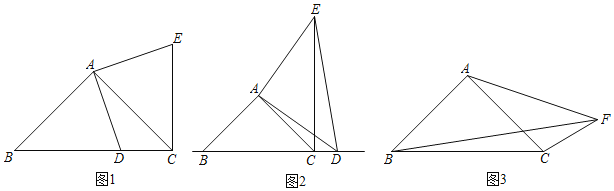
【题目】(1)问题发现:如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B、C重合)将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BD与CE的数量关系是 ,位置关系是 ;
(2)探究证明:如图2,在Rt△ABC与Rt△ADE中,AB=AC,AD=AE,将△ADE绕点A旋转,使点D落在BC的延长线上时,连接EC,写出此时线段AD,BD,CD之间的等量关系,并证明;
(3)拓展延仲:如图3,在四边形ABCF中,∠ABC=∠ACB=∠AFC=45°.若BF=13,CF=5,请直接写出AF的长.
【答案】(1)BD=CE,BD⊥CE;(2)2AD2=BD2+CD2,理由详见解析;(3)![]() .
.
【解析】
(1)证明△BAD≌△CAE,根据全等三角形的性质解答;
(2)证明△BAD≌△CAE,得到BD=CE,根据勾股定理计算即可;
(3)如图3,作辅助线,构建全等三角形,证明△BAF≌△CAG,得到CG=BF=13,证明![]() 是直角三角形,根据勾股定理计算即可.
是直角三角形,根据勾股定理计算即可.
解:(1)在Rt△ABC中,AB=AC,
∴∠B=∠ACB=90°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
∵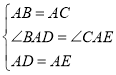 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∵∠ACB=45°,
∴![]() ,
,
故答案为:BD=CE,BD⊥CE;
(2)2AD2=BD2+CD2,理由是:如图2,

∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
∵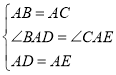 ,
,
∵△BAD≌△CAE(SAS),
∴BD=CE,∠B=∠ACE=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
∴DE2=CE2+CD2,
∵AD=AE,∠DAE=90°,
∴![]() ,
,
∴2AD2=BD2+CD2;
(3)如图3,将AF绕点A逆时针旋转90°至AG,连接CG、FG,
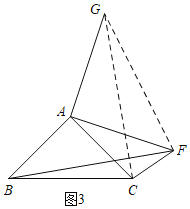
则△FAG是等腰直角三角形,
∴∠AFG=45°,
∵∠AFC=45°,
∴∠GFC=90°,
同理得:△BAF≌△CAG,
∴CG=BF=13,
Rt△CGF中,∵CF=5,
∴FG=12,
∵△FAG是等腰直角三角形,
∴![]() .
.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
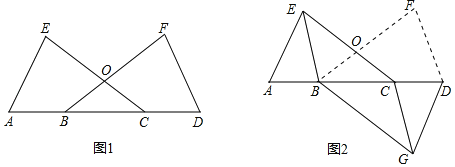
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来一些搜题软件(作业帮,小猿搜题等)陆续进入学生视野,并受到学生的追捧;只需轻松一拍,答案立马浮现,但各界人士关于学生使用搜题软件的利弊的讨论从未停息,某校为了解本校学生使用搜题软件的情况(分为“总是、较多、较少、不用四种情况),就“是否会使用搜题软件辅助完成作业”随机在九年级抽取了部分学生进行调查,绘制成如下不完整的统计图请根据图中信息,回答下列问题:
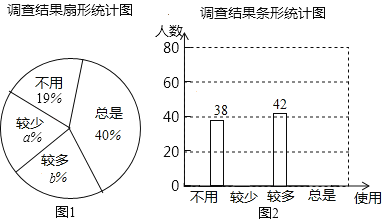
(1)本次接受调查的学生有 名,图1中的a= ,b= ;
(2)“较少”对应的圆心角的度数为 .
(3)请补全条形统计图;
(4)若该校九年级共有1500名学生,请估计其中使用搜题软件辅助完成作业为“较多”的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
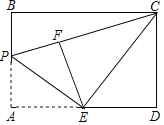
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P(m,n)在抛物线y=ax2-4ax(a>0)上,E为抛物线的顶点.

(1)求点E的坐标(用含a的式子表示);
(2)若点P在第一象限,线段OP交抛物线的对称轴于点C,过抛物线的顶点E作x轴的平行线DE,过点P作x轴的垂线交DE于点D,连接CD,求证:CD∥OE;
(3)如图2,当a=1,且将图1中的抛物线向上平移3个单位,与x轴交于A、B两点,平移后的抛物线的顶点为Q,P是其x轴上方的对称轴上的动点,直线AP交抛物线于另一点D,分别过Q、D作x轴、y轴的平行线交于点E,且∠EPQ=2∠APQ,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板如图所示,叠放在一起.若固定△AOB,将△ACD绕着公共点A按顺时针方向旋转α度(0<α<180).请你探索,当△ACD的一边与△AOB的一边平行时,相应的旋转角α的度数_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com