
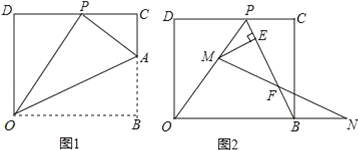
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬OĪŖŌµć£¬µćBŌŚxÖįµÄÕż°ėÖįÉĻ£¬D£Ø0£¬8£©£¬½«¾ŲŠĪOBCDÕŪµž£¬Ź¹µĆ¶„µćBĀäŌŚCD±ßÉĻµÄPµć“¦£®
£Ø1£©ČēĶ¼¢Ł£¬ŅŃÖŖÕŪŗŪÓė±ßBC½»ÓŚµćA£¬ČōOD=2CP£¬ĒóµćAµÄ×ų±ź£®
£Ø2£©ČōĶ¼¢ŁÖŠµÄµć P Ē”ŗĆŹĒCD±ßµÄÖŠµć£¬Ēó”ĻAOBµÄ¶ČŹż£®
£Ø3£©ČēĶ¼¢Ś£¬ŌŚ£ØI£©µÄĢõ¼žĻĀ£¬²ĮČ„ÕŪŗŪAO£¬Ļ߶ĪAP£¬Į¬½ÓBP£¬¶ÆµćMŌŚĻ߶ĪOPÉĻ£ØµćMÓėP£¬O²»ÖŲŗĻ£©£¬¶ÆµćNŌŚĻ߶ĪOBµÄŃÓ³¤ĻßÉĻ£¬ĒŅBN=PM£¬Į¬½ÓMN½»PBÓŚµćF£¬×÷ME”ĶBPÓŚµćE£¬ŹŌĪŹµ±µćM£¬NŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪEFµÄ³¤¶ČŹĒ·ń·¢Éś±ä»Æ£æČō±ä»Æ£¬ĖµĆ÷ĄķÓÉ£»Čō²»±ä£¬Ēó³öĻ߶ĪEFµÄ³¤¶Č£ØÖ±½ÓŠ“³ö½į¹ū¼“æÉ£©.
”¾“š°ø”æ£Ø1£©A£Ø10£¬5£©£»£Ø2£©”ĻAOB=30”ć£»£Ø3£©Ļ߶ĪEFµÄ³¤¶Č²»±ä£¬ĖüµÄ³¤¶ČĪŖ2![]() £®
£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÉčOB=OP=DC=x£¬ŌņDP=x©4£¬ŌŚRt”÷ODPÖŠ£¬øł¾ŻOD2+DP2=OP2£¬½āµĆ£ŗx=10£¬Č»ŗóøł¾Ż”÷ODP”×”÷PCAµĆµ½AC=![]() =3£¬“Ó¶ųµĆµ½AB=5£¬±ķŹ¾³öµćA£Ø10£¬5£©£»
=3£¬“Ó¶ųµĆµ½AB=5£¬±ķŹ¾³öµćA£Ø10£¬5£©£»
£Ø2£©øł¾ŻµćPĒ”ŗĆŹĒCD±ßµÄÖŠµćÉčDP=PC=y£¬ŌņDC=OB=OP=2y£¬ŌŚRt”÷ODPÖŠ£¬øł¾ŻOD2+DP2=OP2£¬½āµĆ£ŗy=![]() £¬Č»ŗóĄūÓĆ”÷ODP”×”÷PCAµĆµ½AC=
£¬Č»ŗóĄūÓĆ”÷ODP”×”÷PCAµĆµ½AC=![]() £¬“Ó¶ųĄūÓĆtan”ĻAOB=
£¬“Ó¶ųĄūÓĆtan”ĻAOB=![]() µĆµ½”ĻAOB=30”ć£»
µĆµ½”ĻAOB=30”ć£»
£Ø3£©×÷MQ”ĪAN£¬½»PBÓŚµćQ£¬Ēó³öMP=MQ£¬BN=QM£¬µĆ³öMP=MQ£¬øł¾ŻME”ĶPQ£¬µĆ³öEQ=![]() PQ£¬øł¾Ż”ĻQMF=”ĻBNF£¬Ö¤³ö”÷MFQ”Õ”÷NFB£¬µĆ³öQF=
PQ£¬øł¾Ż”ĻQMF=”ĻBNF£¬Ö¤³ö”÷MFQ”Õ”÷NFB£¬µĆ³öQF=![]() QB£¬ŌŁĒó³öEF=
QB£¬ŌŁĒó³öEF=![]() PB£¬ÓÉ£Ø1£©ÖŠµÄ½įĀŪĒó³öPB£¬×īŗó“śČėEF=
PB£¬ÓÉ£Ø1£©ÖŠµÄ½įĀŪĒó³öPB£¬×īŗó“śČėEF=![]() PB¼“æÉµĆ³öĻ߶ĪEFµÄ³¤¶Č²»±ä£®
PB¼“æÉµĆ³öĻ߶ĪEFµÄ³¤¶Č²»±ä£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßD£Ø0£¬8£©£¬”ąOD=BC=8£¬
”ßOD=2CP£¬”ąCP=4£¬
ÉčOB=OP=DC=x£¬ŌņDP=x©4£¬
ŌŚRt”÷ODPÖŠ£¬OD2+DP2=OP2£¬¼“£ŗ82+£Øx©4£©2=x2£¬½āµĆ£ŗx=10£¬
”ß”ĻOPA=”ĻB=90”ć£¬”ą”÷ODP”×”÷PCA£¬”ąOD£ŗPC=DP£ŗCA£¬
”ą8£ŗ4=£Øx©4£©£ŗAC£¬ŌņAC=![]() =3£¬
=3£¬
”ąAB=5£¬
”ąµćA£Ø10£¬5£©£»
£Ø2£©”ßµć P Ē”ŗĆŹĒCD±ßµÄÖŠµć£¬
ÉčDP=PC=y£¬ŌņDC=OB=OP=2y£¬
ŌŚRt”÷ODPÖŠ£¬OD2+DP2=OP2£¬¼“£ŗ82+y2=£Ø2y£©2£¬½āµĆ£ŗy=![]() £¬
£¬
”ß”ĻOPA=”ĻB=90”ć£¬”ą”÷ODP”×”÷PCA£¬”ąOD£ŗPC=DP£ŗCA£¬”ą8£ŗy=y£ŗAC£¬
ŌņAC=![]() £¬”ąAB=8©
£¬”ąAB=8©![]() =
=![]() £¬
£¬
”ßOB=2y=![]() £¬”ątan”ĻAOB=
£¬”ątan”ĻAOB=![]() =
=![]() =
=![]() £¬
£¬
”ą”ĻAOB=30”ć£»
£Ø3£©×÷MQ”ĪAN£¬½»PBÓŚµćQ£¬ČēĶ¼2£¬
”ßAP=AB£¬MQ”ĪAN£¬”ą”ĻAPB=”ĻABP=”ĻMQP£¬”ąMP=MQ£¬
”ßBN=PM£¬”ąBN=QM£®
”ßMP=MQ£¬ME”ĶPQ£¬”ąEQ=![]() PQ£®
PQ£®
”ßMQ”ĪAN£¬”ą”ĻQMF=”ĻBNF£¬
ŌŚ”÷MFQŗĶ”÷NFBÖŠ£¬  £¬”ą”÷MFQ”Õ”÷NFB£ØAAS£©£®
£¬”ą”÷MFQ”Õ”÷NFB£ØAAS£©£®
”ąQF=![]() QB£¬
QB£¬
”ąEF=EQ+QF=![]() PQ+
PQ+![]() QB=
QB=![]() PB£¬
PB£¬
ÓÉ£Ø1£©ÖŠµÄ½įĀŪæÉµĆ£ŗPC=4£¬BC=8£¬”ĻC=90”ć£¬
”ąPB=![]() =4
=4![]() £¬
£¬
”ąEF=![]() PB=2
PB=2![]() £¬
£¬
”ąŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬µ±µćM”¢NŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪEFµÄ³¤¶Č²»±ä£¬ĖüµÄ³¤¶ČĪŖ2![]() £®
£®




| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”ææŖѧĒ°£¬ĄīŗĘČ„ÉĢ³”ĀņŹé°ü£¬ÉĢ³”ŌŚøć“ŁĻś»ī¶Æ£¬ĀņŅ»øöŹé°üæÉŅŌĶعż³é½±ŠĪŹ½ĖĶ±Ź£®·½·ØČēĻĀ£ŗŌŚŅ»øö²»ĶøĆ÷µÄĻä×ÓĄļ£¬·Ö±š×°ÓŠĖÄÕÅĶźČ«Ņ»ŃłµÄæØʬ£¬ÉĻĆę·Ö±šŠ“ÓŠ”°øÖ±Ź”±”¢ ”°Ō²Ö鱏”±”¢”°Ē¦±Ź”±”¢”°Š»Š»”±×ÖŃł£ØĘäÖŠ”°Š»Š»”±æؼ“ŅāĪ¶×Åƻӊ½±Ę·£©£®Ę¾³éČ”µÄæØʬ£¬¹¤×÷ČĖŌ±¼“Ź±¶ŌÓ¦µŲøų³ö½±Ę·£®ĄīŗĘĀņĮĖŅ»øöŹé°ü£¬²¢²Ī¼ÓĮĖ³é½±£®
£Ø£±£©ČōÖ»×¼³éŅ»“Ī£¬ĒŅĆæ“ĪÖ»ÄܳéŅ»ÕÅ£¬Ö±½ÓŠ“³öĄīŗĘÄܳ鵽Ņ»Ö§±ŹµÄøÅĀŹ£»
£Ø£²£©ČōæÉŅŌ²»·Å»ŲµŲ³éĮ½“Ī£¬Ćæ“ĪÖ»ÄܳéŅ»ÕÅ£¬ĒėÓĆŹ÷ŠĪĶ¼°ŃĖłÓŠæÉÄܵÄĒéæö±ķŹ¾³öĄ“£¬²¢ĒóĄīŗʵƵ½øÖ±ŹŗĶŌ²Ö鱏µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄĆ껿ĪŖ1£¬ŌņŅŌĻąĮŚĮ½±ßÖŠµćĮ¬ĻßEFĪŖ±ßµÄÕż·½ŠĪEFGHµÄÖܳ¤ĪŖ£Ø £©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£ŗŅŃÖŖŌŚ”÷ABCÖŠ£¬AB=AC£¬DĪŖBC±ßµÄÖŠµć£¬¹żµćD×÷DE”ĶAB£¬DF”ĶAC£¬£¬“¹×ć·Ö±šĪŖE£¬F.
(1)ĒóÖ¤£ŗ”÷BED”Õ”÷CFD£»
(2)Čō”ĻA=90”ć£¬ĒóÖ¤£ŗĖıߊĪDFAEŹĒÕż·½ŠĪ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
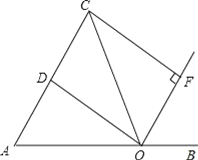
”¾ĢāÄæ”æČēĶ¼£¬µćOŹĒĻ߶ĪABÉĻµÄŅ»µć£¬OA=OC£¬ODĘ½·Ö”ĻAOC½»ACÓŚµćD£¬OFĘ½·Ö”ĻCOB£¬CF”ĶOFÓŚµćF£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪCDOFŹĒ¾ŲŠĪ£»
£Ø2£©µ±”ĻAOC¶ąÉŁ¶ČŹ±£¬ĖıߊĪCDOFŹĒÕż·½ŠĪ£æ²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潫µćMĻņ×óĘ½ŅĘ3øöµ„Ī»³¤¶ČŗóµÄ×ų±źŹĒ£Ø-2£¬1£©£¬ŌņµćMµÄ×ų±źŹĒ£Ø £©
A. £Ø-2£¬4£©B. £Ø-5£¬1£©C. £Ø1£¬1£©D. £Ø-2£¬-4£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµćP(0£¬m)ŌŚyÖįµÄøŗ°ėÖįÉĻ£¬ŌņµćM(£m£¬£m£«1)ŌŚ(””””)
A. µŚŅ»ĻóĻŽB. µŚ¶žĻóĻŽC. µŚČżĻóĻŽD. µŚĖÄĻóĻŽ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”ĻśŹŪŅ»Åś³ÄÉĄ£¬Ę½¾łĆæĢģæÉŹŪ³ö20¼ž£¬Ć漞ÓÆĄū40ŌŖ£¬ĪŖĮĖĄ©“óĻśŹŪ£¬Ōö¼ÓĄūČ󣬾”Įæ¼õÉŁæā“ę£¬ÉĢ³”¾ö¶Ø²ÉČ”ŹŹµ±µÄ½µ¼Ū“ėŹ©£¬¾µ÷²é·¢ĻÖ£¬Čē¹ūĆ漞³ÄÉĄ½µ¼Ū1ŌŖ£¬ÉĢ³”Ę½¾łĆæĢģæɶąŹŪ³ö2¼ž£¬ČōÉĢ³”ĆæĢģŅŖ»ńĄūČó1200ŌŖ£¬Ēė¼ĘĖć³öĆ漞³ÄÉĄÓ¦½µ¼Ū¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com