
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,函数图象与
,函数图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而增大?若存在,求
的增大而增大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)2;(2)![]() ;(3)不存在.
;(3)不存在.
【解析】
(1)根据条件,抛物线化为:y=﹣x2+bx﹣b+1,由△=0即可解决问题.
(2)根据条件,抛物线化为:y=ax2﹣(a+1)x+1,令y=0求出点B横坐标即可.
(3)不存在.由题意:z=y﹣m2x=x2﹣(c+1+m2)x+c,根据对称轴的位置即可判断.
(1)把点A(1,0)代入y=ax2+bx+c得:a+b+c=0.
∵a=﹣1,∴c=﹣b+1,∴抛物线为y=﹣x2+bx﹣b+1,由题意△=0,∴b2﹣4b+4=0,∴(b﹣2)2=0,∴b=2.
(2)∵b=﹣a﹣c,c=1,∴抛物线为y=ax2﹣(a+1)x+1,令y=0,则有ax2﹣(a+1)x+1=0,∴(x﹣1)(ax﹣1)=0,∴x=1或![]() .
.
∵0<a<1,∴![]() >1,∴B点的横坐标为xB>1.
>1,∴B点的横坐标为xB>1.
(3)不存在.理由如下:
∵b=﹣a﹣c,a=1,∴b=﹣1﹣c,∴抛物线为y=x2﹣(c+1)x+c,∴z=y﹣m2x=x2﹣(c+1+m2)x+c.
∵对称轴x=![]() .
.
又∵c≥3,m2≥0,∴对称轴x>0,∴当0<x<![]() 时,z随x的增大而减小,∴这样的m不存在.
时,z随x的增大而减小,∴这样的m不存在.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
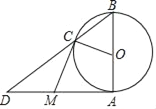
【题目】如图,AB是⊙O的直径,且AB=6,点M为⊙O外一点,且MA,MC分别切⊙O于点A、C.点D是两条线段BC与AM延长线的交点.
(1)求证:DM=AM;
(2)直接回答:
①当CM为何值时,四边形AOCM是正方形?
②当CM为何值时,△CDM为等边三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)求AD的长.
(2)求树长AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:![]() 、例如18可以分解成1×18,2×9,3×6这三种,这时就有
、例如18可以分解成1×18,2×9,3×6这三种,这时就有![]() .给出下列关于F(n)的说法:(1)
.给出下列关于F(n)的说法:(1)![]() ;(2)
;(2)![]() ;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
;(3)F(27)=3;(4)若n是一个整数的平方,则F(n)=1.其中正确说法的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 在
在![]() 边上,点
边上,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等.
的距离相等.

(1)利用尺规作图作出点![]() ,不写作法但保留作图痕迹:
,不写作法但保留作图痕迹:
(2)连接![]() ,若
,若![]() 的底边长为
的底边长为![]() ,周长为
,周长为![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点B逆时针旋转,得
绕点B逆时针旋转,得![]() ,点A,O旋转后的对应点为
,点A,O旋转后的对应点为![]() ,
,![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(2)如图![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在![]() 的条件下,边OA上的一点P旋转后的对应点为
的条件下,边OA上的一点P旋转后的对应点为![]() ,当
,当![]() 取得最小值时,求点
取得最小值时,求点![]() 的坐标
的坐标![]() 直接写出结果即可
直接写出结果即可![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
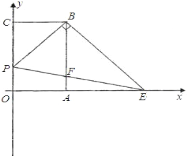
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com