
【题目】如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为 . 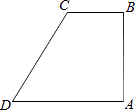
【答案】2或2 ![]() 或4
或4
【解析】解:如图,连接AC.
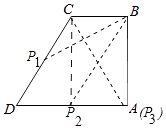
∵BC∥AD,∠DCB=120°,
∴∠D+∠DCB=180°,
∴∠D=60°,
∵DC=DA,
∴△ACD是等边三角形,
∴∠DAC=60°,
∵AB⊥BC,
∴∠CBA=∠BAD=90°,
∴∠BAC=30°,
∴当P3与A重合时,∠BP3C=30°,此时CP3=4,
作CP2⊥AD于P2,则四边形BCP2A是矩形,
易知∠CP2B=30°,此时CP2=2 ![]() ,
,
当CB=CP1时,∠CP1B=∠CBP1=30°,此时CP1=2,
综上所述,CP的长为2或2 ![]() 或4.
或4.
所以答案是2或2 ![]() 或4.
或4.
【考点精析】本题主要考查了含30度角的直角三角形和勾股定理的概念的相关知识点,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣2.8+(﹣3.6)+(+3)﹣(﹣3.6)
(2)(﹣4)2010×(﹣0.25)2009+(﹣12)×(![]() ﹣
﹣![]() +
+![]() )
)
(3)13°16'×5﹣19°12'÷6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣4x﹣m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两个实数根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E为CD中点,连接AE,且AE=2
,E为CD中点,连接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,则BF=( )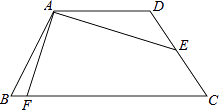
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一下正方形.
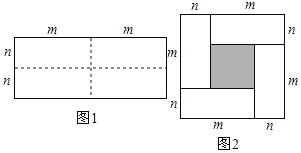
(1)请你用两种不同的方法求图2中阴影部分的面积?
① ②
(2)观察图2,写出三个代数式(m+n)2,(m﹣n)2,4mn之间的等量关系:
(3)根据(2)中的等量关系,解决如下问题:若|a+b﹣7|+|ab﹣6|=0,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
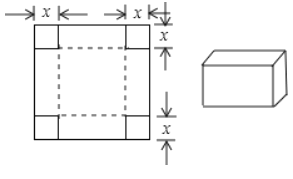
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,定义直线
中,定义直线 ![]() 与双曲线
与双曲线 ![]() 的交点
的交点 ![]() (m、n为正整数)为 “双曲格点”,双曲线
(m、n为正整数)为 “双曲格点”,双曲线 ![]() 在第一象限内的部分沿着竖直方向平移或以平行于
在第一象限内的部分沿着竖直方向平移或以平行于 ![]() 轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.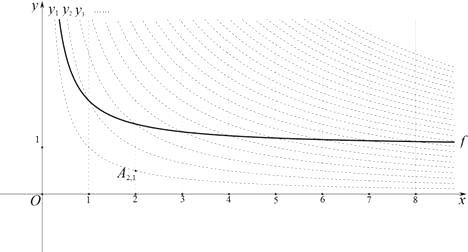
(1)①“双曲格点” ![]() 的坐标为;
的坐标为;
②若线段 ![]() 的长为1个单位长度,则n=;
的长为1个单位长度,则n=;
(2)图中的曲线 ![]() 是双曲线
是双曲线 ![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点 ![]() ,则
,则 ![]() 的解析式为 y=;
的解析式为 y=;
(3)画出双曲线 ![]() 的“派生曲线”g(g与双曲线
的“派生曲线”g(g与双曲线 ![]() 不重合),使其经过“双曲格点”
不重合),使其经过“双曲格点” ![]() 、
、 ![]() 、
、 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com