
【题目】新冠肺炎疫情期间,甲、乙两家网店以同样价格销售相同的防疫用品,它们的优惠方案分别为:甲店,一次性购物中超过100元后的价格部分打七折;乙店,一次性购物中超过500元后的价格部分打五折,设商品原价为![]() 元(
元(![]() ),购物应付金额为
),购物应付金额为![]() 元.
元.
(1)求出在甲店购物时![]() 与
与![]() 之间的函数解析式;
之间的函数解析式;
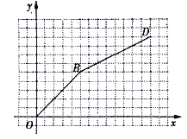
(2)在乙店购物时![]() 与
与![]() 之间的函数图像如图所示(图中线段
之间的函数图像如图所示(图中线段![]() 、射线
、射线![]() ),请在图中画出(l)中所得函数当
),请在图中画出(l)中所得函数当![]() 时的图像,并分别写出该图像与图中
时的图像,并分别写出该图像与图中![]() 、
、![]() 的交点
的交点![]() 和
和![]() 的坐标;
的坐标;
(3)根据函数图像,请直接写出新冠肺炎疫情期间选择哪家网店购物更优惠.
【答案】(1)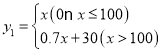 ;(2)图像见解析,A(100,100),B(1100,800);(3)当0<x≤100时,在甲、乙两网店购物花费一样;当100<x<1100时,在甲网店购物更优惠;当x> 1100时,在乙网店购物更优惠.
;(2)图像见解析,A(100,100),B(1100,800);(3)当0<x≤100时,在甲、乙两网店购物花费一样;当100<x<1100时,在甲网店购物更优惠;当x> 1100时,在乙网店购物更优惠.
【解析】
(1)分0<x≤100和x>100两种情况列函数解析式即可;
(2)通过描点、连线即可画出图像;然后列出乙店购物时y2与x之间的函数解析式,联立方程组可得A、C两点的坐标;
(3)根据函数图像在坐标系中的位置即可确定什么情况下,那个店更优惠.
解:(1)当0<x≤100时,y=x;
当x>100时,y=100+0.7(x-100)=0.7x+30;
∴在甲店购物时y与x之间的函数解析式为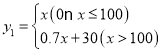 ;
;
(2)当x> 100时,y1,与x的函数图像如下:
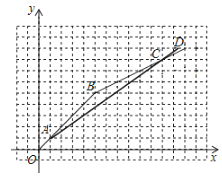
同(1)可得:在乙店购物时y2与x之间的函数解析式为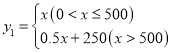
联立方程组 ,解得:
,解得:![]()
所以点A的坐标为(100,100)
联立方程组![]() ,解得:
,解得:![]()
所以点C的坐标为(1100,800);
(3)由函数图像可知,当0<x≤100时,在甲、乙两网店购物花费一样;
当100<x<1100时,在甲网店购物更优惠;
当x> 1100时,在乙网店购物更优惠.


科目:初中数学 来源: 题型:
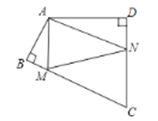
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A.140°B.130°C.120°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
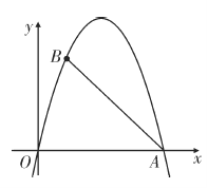
【题目】如图,抛物线![]() 过坐标原点和
过坐标原点和![]() ,
,![]() 两点.
两点.
(1)求该抛物线的表达式;
(2)在线段![]() 右侧的抛物线上是否存在一点
右侧的抛物线上是否存在一点![]() ,使得
,使得![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出点
两部分?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() 为
为![]() 边上任意点,
边上任意点,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() .
.
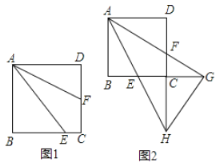
(1)如图1,当点![]() 恰好为
恰好为![]() 中点,延长
中点,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;
;
(2)在(1)的条件下,求证:![]() ;
;
(3)如图2,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
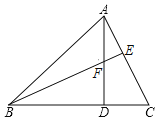
【题目】已知锐角△ABC,∠ABC=45°,AD⊥BC于D,BE⊥AC于E,交AD于F.
(1)求证:△BDF≌△ADC;
(2)若BD=4,DC=3,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点I为△ABC的内心,AB=4cm,AC=3cm,BC=2cm,将∠ACB平移,使其顶点与点I重合,则图中阴影部分的周长为( )
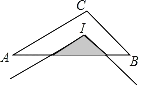
A.1cmB.2cmC.3cmD.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
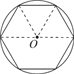
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈![]() =
=![]() =3,那么当n=12时,π≈
=3,那么当n=12时,π≈![]() ≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
≈________(结果精确到0.01,参考数据:sin15°=cos75°≈0.259).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com