天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
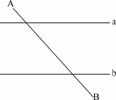
如图，已知直线a//b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB=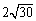
.试在直线a上找一点M，在直线b上找一点N，满足
MN⊥a且AM+MN+NB的长度和最短，则此时AM+NB=（ ）
A．6 B．8 C．10 D．12
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
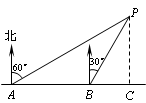
如图，小明同学在东西走向的文一路A处，测得一处公共自行车租用服务点P在北偏东60°方向上，在A处往东90米的B处，又测得该服务点P在北偏东30°方向上，则该服务点P到文一路的距离PC为（ ）
A．60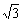
米 B．45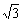米 C．30米 D．45米 
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中，有一张矩形纸片OABC，已知O（0,0），A（4，0），C（0，3），点P是OA边上的动点（与点O、A不重合），现将
PAB沿PB翻折，得到PDB；再在OC边上选取适当的点E，将POE沿PE翻折，得到PFE，并使直线PD、PF重合。
（1）设P（x，0），E（0，y），求y关于x的函数关系式及自变量x的取值范围，并求出y的最大值；
（2）如图
，若翻折后点D落在BC边上，求过点P、B、E的抛物线的函数关系式；
|
|
PEQ是以PE为直角边的直角三角形？若不存在，说明理由；若存在，求出点Q的坐标。
②
查看答案和解析>>
科目：初中数学 来源： 题型：
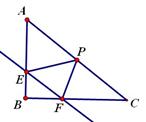
已知Rt△ABC,∠B=90°，直线EF分别于两直角边AB、AC交于E、F两点，且EF//AC。P是斜边AC的中点，连接PE、PF，且已知AB=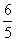
,BC=
。
（1） 如图1，当E、F均为两直角边中点时，求证：四边形EPFB是矩形，并求出此时EF的长。
（2） 如图2，设EF的长度为x（x>0）,当sin∠EPF=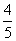
（∠EPF为锐角）时，用含x的代数式表示EP的长度。
（3） 记△PEF 的面积为S，则当EP为多少时，S的值最大，并求出该最大值。
查看答案和解析>>
科目：初中数学 来源： 题型：
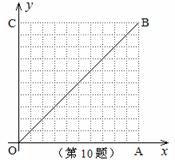
如图，在10×10的网格中，每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点。若抛物线经过图中的三个格点，则以这三个格点为顶点的三角形称为抛物
线的“内接格点三角形”。以O为坐标原点建立如图所示的平面直角坐标系，若抛物线与网格对角线OB的两个交点之间的距离为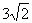
，且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点，则满足上述条件且对称轴平行于
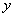轴的抛物线条数是（ ）
A. 16 B. 15 C. 14 D. 13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的化简结果为………………………………………………( )
C．
D．
-
