
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
(1)填空:点C的坐标为( , ),点D的坐标为( , );
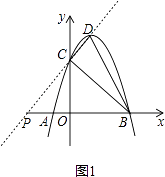
(2)设点P的坐标为(a,0),当|PD﹣PC|最大时,求α的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
【答案】
(1)0,3,1,4
(2)解:∵在三角形中两边之差小于第三边,
∴延长DC交x轴于点P,
设直线DC的解析式为y=kx+b,把D、C两点坐标代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直线DC的解析式为y=x+3,
将点P的坐标(a,0)代入得a+3=0,求得a=﹣3,
如图1,点P(﹣3,0)即为所求;
(3)解:过点C作CE∥x,交直线BD于点E,如图2,

由(2)得直线DC的解析式为y=x+3,
可求得直线BD的解析式为y=﹣2x+6,直线BC的解析式为y=﹣x+3,
在y=﹣2x+6中,当y=3时,x= ![]() ,
,
∴E点坐标为( ![]() ,3),
,3),
设直线P′C′与直线BC交于点M,
∵P′C′∥DC,P′C′与y轴交于点(0,3﹣t),
∴直线P′C′的解析式为y=x+3﹣t,
联立 ![]() ,解得
,解得 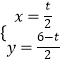 ,
,
∴点M坐标为( ![]() ,
, ![]() ),
),
∵B′C′∥BC,B′坐标为(3+t,0),
∴直线B′C′的解析式为y=﹣x+3+t,
分两种情况讨论:
①当0<t< ![]() 时,如图2,B′C′与BD交于点N,
时,如图2,B′C′与BD交于点N,
联立 ![]() ,解得
,解得 ![]() ,
,
∴N点坐标为(3﹣t,2t),
S=S△B′C′P﹣S△BMP﹣S△BNB′= ![]() ×6×3﹣
×6×3﹣ ![]() (6﹣t)×
(6﹣t)× ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() t×2t=﹣
t×2t=﹣ ![]() t2+3t,
t2+3t,
其对称轴为t= ![]() ,可知当0<t<
,可知当0<t< ![]() 时,S随t的增大而增大,当t=
时,S随t的增大而增大,当t= ![]() 时,有最大值
时,有最大值 ![]() ;
;
②当 ![]() ≤t<6时,如图3,直线P′C′与DB交于点N,
≤t<6时,如图3,直线P′C′与DB交于点N,
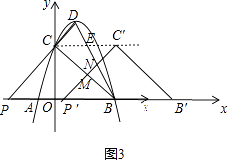
联立 ![]() ,解得
,解得 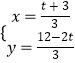 ,
,
∴N点坐标为( ![]() ,
, ![]() ),
),
S=S△BNP′﹣S△BMP′= ![]() (6﹣t)×
(6﹣t)× ![]() ﹣
﹣ ![]() ×(6﹣t)×
×(6﹣t)× ![]() =
= ![]() (6﹣t)2=
(6﹣t)2= ![]() t2﹣t+3;
t2﹣t+3;
显然当 ![]() <t<6时,S随t的增大而减小,当t=
<t<6时,S随t的增大而减小,当t= ![]() 时,S=
时,S= ![]()
综上所述,S与t之间的关系式为S=  ,且当t=
,且当t= ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]() .
.
【解析】解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴C(0,3),D(1,4),
所以答案是:0;3;1;4;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学胜.
(1)当x=3时,谁获胜的可能性大?
(2)当x为何值时,游戏对双方是公平的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 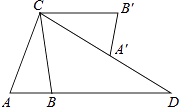
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式因式分解.例如:![]() ,
,![]() 都是因式分解.因式分解也可称为分解因式.
都是因式分解.因式分解也可称为分解因式.
材料2:只含有一个未知数,且未知数的最高次数是![]() 的整式方程称作一元二次方程.一元二次方程的般形式是:
的整式方程称作一元二次方程.一元二次方程的般形式是:![]() (其中
(其中![]() ,
,![]() ,
,![]() 为常数且
为常数且![]() ).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
).“转化”是一种重要的数学思想方法,我们可以利用因式分解把部分一元二次方程转化为一元一次方程求解.
例如解方程;![]()
![]()
![]()
![]() 或
或![]()
![]() 原方程的解是
原方程的解是![]() ,
,![]()
∴原方程的解是![]() ,
,![]()
又如解方程:![]()
![]()
![]()
![]()
![]() 原方程的解是
原方程的解是![]()
请阅读以上材料回答以下问题:
(1)若![]() ,则
,则![]() _______;
_______;![]() _______;
_______;
(2)请将下列多项式因式分解:
![]() _______,
_______,![]() ________;
________;
(3)在平面直角坐标系中,已知点![]() ,
,![]() ,其中
,其中![]() 是一元二次方程
是一元二次方程![]() 的解,
的解,![]() 为任意实数,求
为任意实数,求![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )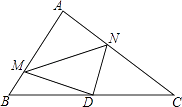
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AC上,点F、G分别在AC、BC的延长线上,CE平分∠ACB交BD于点O,且∠EOD+∠OBF=180°,∠F=∠G.则图中与∠ECB相等的角有( )
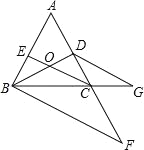
A. 6个 B. 5个 C. 4个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正确的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
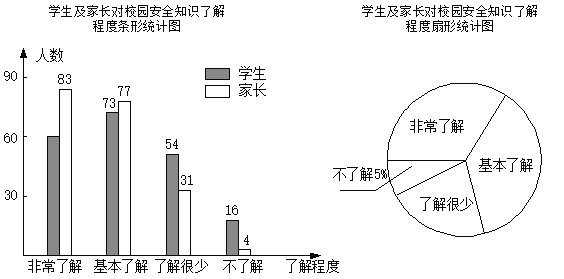
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com