
 已知抛物线y=-x2+2x+3与y轴交于点C,过O作直线交抛物线于M,N两点,是否存在这样的一条直线MN,使得△CMN的内心在y轴上?若存在,求出直线MN的解析式;若不存在,请说明理由.
已知抛物线y=-x2+2x+3与y轴交于点C,过O作直线交抛物线于M,N两点,是否存在这样的一条直线MN,使得△CMN的内心在y轴上?若存在,求出直线MN的解析式;若不存在,请说明理由. 分析 设直线MN:y=kx,则假设M(m,km),N(n,kn),因为点M、N在抛物线上,则M(m,-m2+2m+3),N(n,-n2+2n+3),所以km=-m2+2m+3,kn=-n2+2n+3,所以m、n是方程:x2+(k-2)x-3=0的两根,得到m+n=2-k,mn=-3,再根据直线CM,直线CN两直线与y轴夹角相等,两直线斜率互为相反数,即和为0,
得到$\frac{3-km}{m}$+$\frac{3-kn}{n}$=0,代入化简解方程即可解决问题.
解答 解:存在.
理由:由题意点C(0,3),设直线MN:y=kx,则假设M(m,km),N(n,kn);
∵点M、N在抛物线上,则M(m,-m2+2m+3),N(n,-n2+2n+3),
∴km=-m2+2m+3,kn=-n2+2n+3,
显然m、n是方程:x2+(k-2)x-3=0的两根,
则m+n=2-k,mn=-3,
∵△CMN的内心在y轴上,
∴直线CM,直线CN两直线与y轴夹角相等,两直线斜率互为相反数,即和为0,
∴$\frac{3-km}{m}$+$\frac{3-kn}{n}$=0,
∴3(m+n)-2kmn=0,
∴6-3k+6k=0,
∴k=-2,
∴直线MN:y=-2x.
点评 本题考查三角形内心、二次函数、一次函数等知识,解题的关键是学会利用参数,构建方程解决问题,学会用转化的思想思考问题,题目比较难,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 80° | B. | 80°或100° | C. | 100° | D. | 160°或20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=0,x2=5 | B. | x1=0,x2=-5 | C. | x1=0,x2=$\frac{1}{5}$ | D. | x1=0,x2=-$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
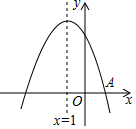 如图,抛物线y=ax2+bx+c与x轴的一个交点是A(1,0),对称轴为直线x=-1,则一元二次方程ax2+bx+c=0的解是x1=1,x2=-3.
如图,抛物线y=ax2+bx+c与x轴的一个交点是A(1,0),对称轴为直线x=-1,则一元二次方程ax2+bx+c=0的解是x1=1,x2=-3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
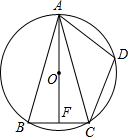 如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为70°,则∠BAF=20度.
如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为70°,则∠BAF=20度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
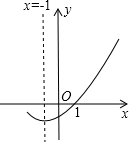 如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分给出下列命题:
如图是二次函数 y=ax2+bx+c(a≠0)的图象的一部分给出下列命题:| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com