
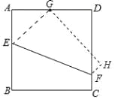
【题目】如图,将边长为4的正方形ABCD沿着折痕EF折叠,使点B落在边AD的中点G处.
(1)求线段BE的长;
(2)连接BF、GF,求证:BF=GF;
(3)求四边形BCFE的面积.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)由折叠的性质可得![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中利用勾股定理求出
中利用勾股定理求出![]() 的值;
的值;
(2)根据折叠的性质即可求解;
(3)四边形![]() 是梯形,要求其面积需要得出
是梯形,要求其面积需要得出![]() 的长,可通过求出
的长,可通过求出![]() 的长度,进行求解.
的长度,进行求解.
(1)由题意,点![]() 与点
与点![]() ,点
,点![]() 与点
与点![]() 分别关于直线
分别关于直线![]() 对称,
对称,
![]()
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 落在边
落在边![]() 的中点
的中点![]() 处,
处,
![]()
![]() ,
,
![]()
![]() ,
,
解得:![]() ,
,
![]()
![]() .
.
(2)![]() 将边长为
将边长为![]() 的正方形
的正方形![]() 沿着折痕
沿着折痕![]() 折叠,使点
折叠,使点![]() 落在边
落在边![]() 的中点
的中点![]() 处,连接BF、GF,在△BFE和△GFE中,BE=GE,∠BEF=∠GEF,EF=EF,∴△BFE≌△GFE
处,连接BF、GF,在△BFE和△GFE中,BE=GE,∠BEF=∠GEF,EF=EF,∴△BFE≌△GFE
![]()
![]() ;
;
(3)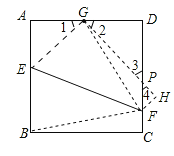
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,![]() ,
,
![]() 点
点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,
边上,
![]() 四边形
四边形![]() 是直角梯形,
是直角梯形,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】综合与实践:在学习了《7.4实践与探索》之后,小亮买了若干块完全相同的长方形拼图(图1),第一次他用2块图1的长方形拼出了图2所示的正方形,第二次他又用4块图1的长方形拼出了图3所示的正方形(中间留有一个正方形小洞,即阴影区域),经过测量,他发现图3的大正方形的边长为![]() .
.

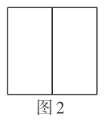

(1)请你帮小亮求出图1中长方形的长和宽;
(2)请你参照图3,用图1的长方形拼出一个面积为![]() 的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个).
的正方形(中间留有一个正方形小洞),请画出你拼出的大正方形(要求画出两个).
查看答案和解析>>
科目:初中数学 来源: 题型:
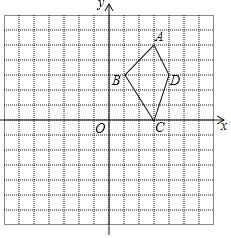
【题目】四边形ABCD在平面直角坐标系的位置如图所示,将四边形ABCD先向下平移2个单位,再向左平移3个单位得到四边形A1B1C1D1,解答下列各题:
(1)请在图中画出四边形A1B1C1D1;
(2)请写出四边形A1B1C1D1的顶点B1、D1坐标;
(3)请求出四边形A1B1C1D1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
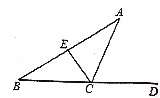
【题目】如图,B、C、D三点在一条直线上,AC平分∠DCE,且与BE的延长线交于点A。
(1)如果∠A=35°,∠B=30°,求∠BEC的度数;
(2)小明经过改变∠A,∠B的度数进行多次探究,得出A、B、BEC三个角之间存在固定的数量关系,请用一个等式表示出这个关系,并进行证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
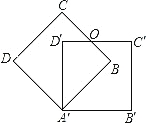
A. 6![]() B. 6C. 3
B. 6C. 3![]() D. 3+3
D. 3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴平行于y轴的抛物线与x轴交于点A、B,与y轴交于点C,过C作CD∥x轴,与抛物线交于点D.若OA=1,CD=4,则线段AB的长为 . 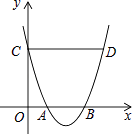
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某船于上午8点在A处观测小岛C在北偏东60°方向上.该船以每小时40海里的速度向东航行到B处,此时测得小岛C在北偏东30°方向上.船以原速度再继续向东航行2小时到达小岛C的正南方D点.求船从A到D一共走了多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.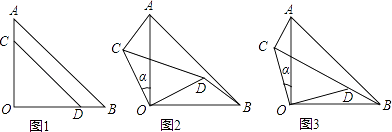
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次试验中,小明把一根弹簧的上端固定,在其下端悬挂物体,测得弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系如下表:
之间的关系如下表:
所挂物体质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 8 | 10 | 12 | 14 | 16 | 18 |
下列说法错误的是( )
A.弹簧的长度随所挂物体质量的变化而变化,所挂物体质量是自变量,弹簧长度是因变量
B.不挂物体时,弹簧的长度为![]()
C.弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系式是
之间的关系式是![]()
D.在弹性限度内,当所挂物体的质量为![]() 时,弹簧的长度为
时,弹簧的长度为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com