
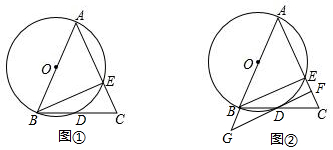
分析 (1)由AB为⊙O的直径,得到∠AEB=90°,根据等腰三角形的性质和三角形的内角和即可得到结论;
(2)连接OD,AD,由FG是⊙O的切线,得到∠ODG=90°,根据三角形的中位线的性质得到OD∥AC,于是得到∠GOD=∠BAC=45°,于是得到结论.
解答 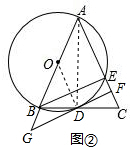 解:(1)∵AB为⊙O的直径,
解:(1)∵AB为⊙O的直径,
∴∠AEB=90°,
∵AE=BE,
∴∠A=∠ABE=$\frac{180°-90°}{2}$=45°,
∵AB=AC,
∴$∠ABC=∠ACB=\frac{180°-45°}{2}$=67.5°,
∴∠EBC=∠ABC-∠ABE=22.5°;
(2)连接OD,AD,∵FG是⊙O的切线,
∴GF⊥OD,
∴∠ODG=90°,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC,
∵OA=OB,
∴OD是△ABC的中位线,
∴OD∥AC,
∴∠GOD=∠BAC=45°,
∵cos∠GOD=$\frac{OD}{OG}=\frac{\sqrt{2}}{2}$,
∵⊙O的直径为10,
∴OB=OD=5,
∴OG=5$\sqrt{2}$,
∴BG=5$\sqrt{2}$-5.
点评 本题考查了切线的性质,圆周角定理,勾股定理,三角函数的定义,三角形的中位线的性质,正确的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
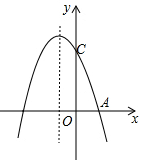 如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)、点B与y轴相交于点C(0,3),下列结论:
如图,抛物线y=-x2+bx+c与x轴交于点A(1,0)、点B与y轴相交于点C(0,3),下列结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.5×10-8s | B. | 5×10-9s | C. | 5×10-8s | D. | 0.5×10-9s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
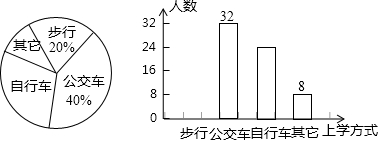
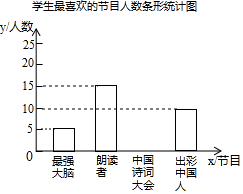 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:| 节目 | 人数(名) | 百分比 |
| 最强大脑 | 5 | 10% |
| 朗读者 | 15 | b% |
| 中国诗词大会 | a | 40% |
| 出彩中国人 | 10 | 20% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com