
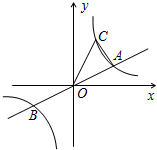
 如图,已知直线y=ax与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,点B的坐标为B(-2,-1),C为双曲线$y=\frac{k}{x}(k>0)$上一点,且在第一象限内.
如图,已知直线y=ax与双曲线$y=\frac{k}{x}(k>0)$交于A、B两点,点B的坐标为B(-2,-1),C为双曲线$y=\frac{k}{x}(k>0)$上一点,且在第一象限内.分析 (1)把B点坐标代入$y=\frac{k}{x}(k>0)$中,可求得k的值;
(2)把B点坐标代入y=ax,可求得a的值,联立直线和双曲线解析式可求得A点坐标,分别过点A、C作x轴的垂线,交x轴于点E、D,设出C点坐标,可表示出△AOC的面积,可得到方程,求解即可.
解答 解:
(1)∵B(-2,-1)在双曲线上,
∴k=-2×(-1)=2,
故答案为:2;
(2)由(1)可知双曲线解析式为y=$\frac{2}{x}$,
把B点坐标代入直线y=ax可得-2a=-1,解得a=$\frac{1}{2}$,
∴直线解析式为y=$\frac{1}{2}$x,
联立直线和双曲线解析式可得$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=\frac{1}{2}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$,
∴A点坐标为(2,1),
∵C点为双曲线上一点,且在第一象限内,
∴可设C点坐标为(x,$\frac{2}{x}$),其中x>0,
如图,分别过点A、C作x轴的垂线,交x轴于点E、D,
则CD=$\frac{2}{x}$,OD=x,OE=2,AE=1,
∴DE=|2-x|,
∴S△AOE=$\frac{1}{2}$OE•AE=$\frac{1}{2}$×2×1=1,S△COD=$\frac{1}{2}$OD•CD=$\frac{1}{2}$x•$\frac{2}{x}$=1,S梯形ACDE=$\frac{1}{2}$(AE+CD)DE=$\frac{1}{2}$(1+$\frac{2}{x}$)|2-x|,
∴S四边形ACOE=S△OCD+S梯形ACDE=1+$\frac{1}{2}$(1+$\frac{2}{x}$)|2-x|,
∴S△AOC=S四边形ACOE-S△AOE,
即$\frac{3}{2}$=1+$\frac{1}{2}$(1+$\frac{2}{x}$)|2-x|-1,
解得x=1或x=4,
∴C点坐标为(1,2)或(4,$\frac{1}{2}$),
故答案为:(1,2)或(4,$\frac{1}{2}$).
点评 本题主要考查函数图象的交点,掌握两函数图象的交点坐标满足每个函数解析式是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{56}{x}=\frac{60}{x-2}$ | B. | $\frac{56}{x-2}=\frac{60}{x}$ | C. | $\frac{56}{x}=\frac{60}{x+2}$ | D. | $\frac{56}{x+2}=\frac{60}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC的三边AB,BC,AC的长分别为45,50,60,其中三条角平分线相交于点O,则S△ABO:S△BCO:S△CAO=9:10:12.
如图,△ABC的三边AB,BC,AC的长分别为45,50,60,其中三条角平分线相交于点O,则S△ABO:S△BCO:S△CAO=9:10:12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}a=2\\ b=3.\end{array}\right.$ | B. | $\left\{\begin{array}{l}a=-2\\ b=3.\end{array}\right.$ | C. | $\left\{\begin{array}{l}a=2\\ b=-3.\end{array}\right.$ | D. | $\left\{\begin{array}{l}a=-2\\ b=-3.\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com