
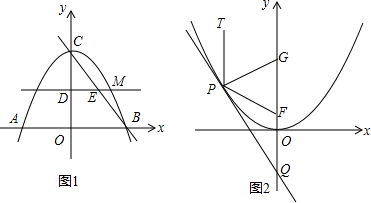
���� ��1�������á�ABC������ֵ���OC�ij����õ���C�����꣬Ȼ�����ô���ϵ������⼴�ɣ�
��2���ı���DOEB������ԲԲ��ΪN������BN��������NG��OD�ڵ�G����NH��OB�ڵ�H�����ı���OHNGΪ�����Σ���NH=X����OH=x��BH=6-x�������ı���DOEB������ԲԲ��ΪN�����ԡ�NBH=$\frac{1}{2}��OBC$������tan��ABC=$\frac{4}{3}$�����tan$\frac{1}{2}��ABC$=$\frac{1}{2}$������$\frac{NH}{BH}=\frac{1}{2}$����$\frac{x}{6-x}=\frac{1}{2}$����ã�x=2����NH=2����������Բ��ֱ��Ϊ4������DM��x�ᣬ��M�������Ϊ��x��4�����ѣ�x��4������������C1�Ľ���ʽ�����ɽ��
��3�������ö��κ�����ͼ���뼸�α任�ó�������C2�Ľ���ʽ������P��m��$\frac{1}{4}$m2����ֱ��PQ�Ľ���ʽΪy=kx+n��k��0��������ֱ��PQ����������һ���������n=-k2��Ȼ����k��ʾ��P��Q��G�����꣬�õ�GF=FQ��������ֱ��������б���ϵ����ߵ����ʣ����������ε����ʺ�ƽ���ߵ����ʽ����������ɣ�
��� �⣺��1����B��6��0���ɵ�OB=6��
��tan��ABC=$\frac{OC}{OB}=\frac{OC}{6}=\frac{4}{3}$��
��OC=8����C��������0��8����
�ߵ�A��B��C������������C1�ϣ�
��$\left\{\begin{array}{l}{\frac{256}{9}a-\frac{16}{3}b+c=0}\\{36a+6b+c=0}\\{c=8}\end{array}\right.$��
��������C1�Ľ���ʽΪy=$-\frac{1}{4}{x}^{2}+\frac{1}{6}x+8$��
��2����ͼ1��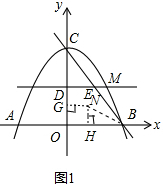
�ı���DOEB������ԲԲ��ΪN������BN��������NG��OD�ڵ�G����NH��OB�ڵ�H��
���ı���OHNGΪ�����Σ���NH=X����OH=x��BH=6-x��
���ı���DOEB������ԲԲ��ΪN��
���NBH=$\frac{1}{2}��OBC$��
��tan��ABC=$\frac{4}{3}$��
��tan��ABC=$\frac{2tan\frac{1}{2}��ABC}{1-��tan\frac{1}{2}��ABC��^{2}}$=$\frac{4}{3}$��
��ã�$tan\frac{1}{2}��ABC=-2$����ȥ����$tan\frac{1}{2}��ABC=\frac{1}{2}$��
��tan��NBH=$\frac{1}{2}$��
��$\frac{NH}{BH}=\frac{1}{2}$��
��$\frac{x}{6-x}=\frac{1}{2}$��
��ã�x=2��
��NH=2��
������Բ��ֱ��Ϊ4��
��OD=4��
��OD=����Բ��ֱ����
��DM��x�ᣬ
����M���������x��4����
�ѣ�x��4������������C1�Ľ���ʽΪy=$-\frac{1}{4}{x}^{2}+\frac{1}{6}x+8$�ã�$-\frac{1}{4}{x}^{2}+\frac{1}{6}x+8=4$��
��ã�x=$\frac{1-\sqrt{145}}{3}$����ȥ����$\frac{1+\sqrt{145}}{3}$��
���M��������$\frac{1+\sqrt{145}}{3}$��4����
��3����������C1����ij����ת180�㣬�õ�����������C2�Ķ���Ϊ����ԭ�㣬
����������C2�Ľ���ʽΪy=$\frac{1}{4}$x2��
��P��m��$\frac{1}{4}$m2����ֱ��PQ�Ľ���ʽΪy=kx+n��k��0����
�ɵ�Q��y�Ḻ������һ�㣬��Q���ֱ��PQ��������C2�ڵڶ�������Ψһ������P����$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=kx+n}\end{array}\right.$��
��$\frac{1}{4}$x2-kx+n=0��
���=��-k��2-4��$\frac{1}{4}$����-n��=0����n=-k2��
��ֱ��PQ�Ľ���ʽΪy=kx-k2��P��2k��k2����Q��0��-k2����
��ֱ��PG�Ľ���ʽΪy=$\frac{1}{4}$x+p����P���������ɵ�p=k2-2����G��0��k2-2����
��GF=k2-1��FQ=k2-1��
��GF=FQ������F��Rt��GPQб���ϵ��е㣬
��FP=FG��
���FPG=��FGP��
�֡�PT��y�ᣬ
���TPG=��FGP��
���TPG=��FPG��
���� ���⿼���˶��κ������ۺ�Ӧ�ã��漰�˴���ϵ������һ�κ��������κ����Ľ���ʽ���ۺ��Խ�ǿ����һ�����Ѷȣ�����ʱҪע�����ν��˼�룬����˼�룬��������˼���Ӧ�ã�


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д� ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
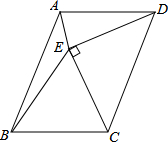 ��ͼ��?ABCD�ı�CDΪб������������ֱ�ǡ�CDE��ʹAD=DE=CE����DEC=90�㣬�ҵ�E��ƽ���ı����ڲ�������AE��BE�����AEB�Ķ�����
��ͼ��?ABCD�ı�CDΪб������������ֱ�ǡ�CDE��ʹAD=DE=CE����DEC=90�㣬�ҵ�E��ƽ���ı����ڲ�������AE��BE�����AEB�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
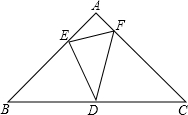 ��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ�
��ABC�ǵ���ֱ�������Σ���A=90�㣬AB=$\sqrt{2}$����Dλ�ڱ�BC���е��ϣ���E��AB�ϣ���F��AC�ϣ���EDF=45�㣬�������½��ۣ�| A�� | �٢ڢ� | B�� | �٢ۢܢ� | C�� | �ڢۢ� | D�� | �ۢܢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
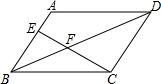 ��ͼ����?ABCD�У�E��AB���ϵ�һ�㣬����CE���Խ���BD��F����AE��BE=2��3�����BEF�͡�DCF���ܳ�֮��Ϊ3��5��
��ͼ����?ABCD�У�E��AB���ϵ�һ�㣬����CE���Խ���BD��F����AE��BE=2��3�����BEF�͡�DCF���ܳ�֮��Ϊ3��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��2��m��3 | B�� | m��3��m��4 | C�� | 2��m��3 | D�� | 3��m��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
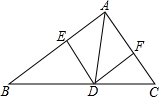 ��ͼ���ڡ�ABC�У�DE��CA��DF��BA�������ĸ��жϲ���ȷ���ǣ�������
��ͼ���ڡ�ABC�У�DE��CA��DF��BA�������ĸ��жϲ���ȷ���ǣ�������| A�� | �ı���AEDF��ƽ���ı��� | |
| B�� | �����BAC=90�㣬��ô�ı���AEDF�Ǿ��� | |
| C�� | ���ADƽ�֡�BAC����ô�ı���AEDF�Ǿ��� | |
| D�� | ���AD��BC����AB=AC����ô�ı���AEDF������ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com