
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.

(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“创卫工作,人人参与”我区园林工作者,为了把城市装扮得更加靓丽,用若干相同的花盆按一定的规律组成不同的正多边形图案.如图,其中第![]() 个图形一共有
个图形一共有![]() 个花盆,第
个花盆,第![]() 个图形一共有
个图形一共有![]() 个花盆,第
个花盆,第![]() 个图形一共有
个图形一共有![]() 个花盆...则第
个花盆...则第![]() 个图形中一共有花盆的个数为( )
个图形中一共有花盆的个数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON![]() 60°,点A是OM边上一点,点B,C是ON边上两点,且AB
60°,点A是OM边上一点,点B,C是ON边上两点,且AB![]() AC,作点B关于OM的对称点点D,连接AD,CD,OD.
AC,作点B关于OM的对称点点D,连接AD,CD,OD.
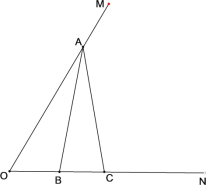

(1)依题意补全图形;
(2)猜想∠DAC![]() °,并证明;
°,并证明;
(3)猜想线段OA、OD、OC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题“在一个三角形中,至少有一个内角小于或等于![]() ”的过程如下:
”的过程如下:
已知: ![]() ;
;
求证: ![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
证明:假设![]() 中没有一个内角小于或等于
中没有一个内角小于或等于![]() ,即
,即![]() ,则
,则
![]() ,
,
这与“__________” 这个定理相矛盾,
所以![]() 中至少有一个内角小于或等于
中至少有一个内角小于或等于![]() .
.
在证明过程中,横线上应填入的句子是( )
A.三角形内角和等于![]() B.三角形的一个外角等于与它不相邻的两个内角的和
B.三角形的一个外角等于与它不相邻的两个内角的和
C.等边三角形的各角都相等,并且每个角都等于![]() D.等式的性质
D.等式的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生共900人,为了解这个年级学生的体能,从中随机抽取部分学生进行1 min的跳绳测试,并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理,下图是这四名同学提供的部分信息:
甲:将全体测试数据分成6组绘成直方图(如图);
乙:跳绳次数不少于105次的同学占96%;
丙:第①、②两组频率之和为0.12,且第②组与第⑥组频数都是12;
丁:第②、③、④组的频数之比为4:17:15。

根据这四名同学提供的材料,下面有四个推断:
①这次跳绳测试共抽取了150人;②该年级跳绳次数的中位数在115~125之间
③第4组的人数为45人 ④如果跳绳次数不少于135次为优秀,根据这次调查结果,估计全年级达到跳绳优秀的人数可以超过250人,其中合理的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 与
与![]() 有公共顶点
有公共顶点![]() (顶点均按逆时针排列),
(顶点均按逆时针排列),![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
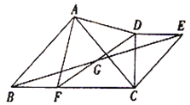
(1)如图,当![]() 时,
时,
求证:①![]() ;
;
②![]() 是等腰直角三角形.
是等腰直角三角形.
(2)当![]() 时,画出相应的图形(画一个即可),并直接指出
时,画出相应的图形(画一个即可),并直接指出![]() 是何种特殊三角形.
是何种特殊三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①四个角都相等的四边形是矩形;②有一组对边平行,有两个角为直角的四边形是矩形;③两组对边分别相等且有一个角为直角的四边形是矩形;④对角线相等且有一个角是直角的四边形是矩形;⑤对角线互相平分且相等的四边形是矩形.其中,正确的个数是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:

![]()
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?
(填“是”或不是);
(2)若某三角形的三边长分别为1、![]() 、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
、2,则该三角形是不是奇异三角形,请做出判断并写出判断依据;
(3)在![]() 中,两边长分别为
中,两边长分别为![]() ,且且
,且且![]() ,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
,则这个三角形是不是奇异三角形?请做出判断并写出判断依据;
探究:Rt![]() 中,
中,![]() ,且b>a,若Rt
,且b>a,若Rt![]() 是奇异三角形,求
是奇异三角形,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com