
分析 根据sin2α+cos2α=1,可得完全平方公式,根据正弦的二倍角公式,可得二次函数,根据二次函数的最值,可得答案.
解答 解:原式=(sin2α+cos2α)2-2sin2αcos2α+sinαcosα
=1-$\frac{1}{2}$sin22α+$\frac{1}{2}$sin2α
=-$\frac{1}{2}$(sin22α-sin2α+$\frac{1}{4}$)+1+$\frac{1}{8}$
=-$\frac{1}{2}$(sin2α-$\frac{1}{2}$)2+$\frac{9}{8}$,
当sin2α=$\frac{1}{2}$时,sin4α+sinα•cosα+cos4α的最大值为$\frac{9}{8}$,
故答案为:$\frac{9}{8}$.
点评 本题考查了二次函数最值,利用据sin2α+cos2α=1得出完全平方公式是解题关键,又利用正弦的二倍角公式,二次函数的性质.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是8,若点B的纵坐标是-1.
如图,在直标系内,一次函数y=kx+b(kb>0,b<0)的图象分别与x轴、y轴和直线x=4相交于A、B、C三点,直线x=4与x轴交于点D,四边形OBCD(O是坐标原点)的面积是8,若点B的纵坐标是-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
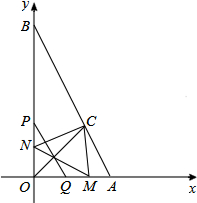 如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).
如图,在平面直角坐标系中,点A(2,0)、B(0,4),∠AOB的平分线交AB于点C,动点P从点O出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,PQ∥AB,交x轴于点Q,过点P、Q作关于直线OC的对称点M,N,连接MC、NC、MN,设点P运动的时间为t(0<t<2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
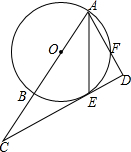 如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF延长线于点D,交AB延长线于点C.
如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直,交AF延长线于点D,交AB延长线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{-a-b}$ | B. | $\frac{a}{a+b}$ | C. | $\frac{a}{-a+b}$ | D. | $\frac{a}{a-b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com