
分析 首先根据零指数幂的运算方法,求出(2$\sqrt{3}$-1)0的值是多少;然后根据负有理数的绝对值是它的相反数,求出|-6|的值是多少;最后把求出的(2$\sqrt{3}$-1)0、|-6|的值相加即可.
解答 解:(2$\sqrt{3}$-1)0+|-6|
=1+6
=7.
故答案为:7.
点评 (1)此题主要考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(2)此题还考查了绝对值的含义和应用,要熟练掌握,解答此题的关键是要明确:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:填空题
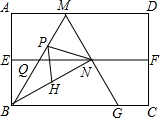 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为EF,展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com