
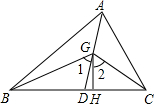
 如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:分析 (1)由三角形内角和定理可知∠ABC+∠ACB=180°-∠BAC,然后利用角平分线的性质即可求出∠BGC=90°+$\frac{1}{2}$∠BAC.
(2)由于AD是它的角平分线,所以∠BAD=∠CAD,然后根据图形可知:∠1=∠BAD+∠ABG,∠2=90°-∠GCH,最后根据三角形的内角和定理以及外角的性质即可求出答案.
解答 解:(1)由三角形内角和定理可知:∠ABC+∠ACB=180°-∠BAC,
∵BG,CG分别平分∠ABC,∠ACB,
∠GBC=$\frac{1}{2}$∠ABC,∠GCB=$\frac{1}{2}$∠ACB
∴∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠BAC)=90°-$\frac{1}{2}$∠BAC
∴∠BGC=180°-(∠GBC+∠GCB)=180°-$\frac{1}{2}$(∠ABC+∠ACB)=90°+$\frac{1}{2}$∠BAC;
(2)∵AD是它的角平分线,
∴∠BAD=∠CAD
∴∠1=∠BAD+∠ABG,
∵GH⊥BC,
∴∠GHC=90°
∴∠2=90°-∠GCH
=90°-$\frac{1}{2}$∠ACB
=90°-$\frac{1}{2}$(180°-∠DAC-∠ADC)
=$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ADC
∵∠ADC=∠ABC+∠BAD,
∴$\frac{1}{2}$∠ADC=$\frac{1}{2}$∠ABC+∠$\frac{1}{2}$∠BAD
=∠ABG+$\frac{1}{2}$∠BAD,
∴∠2=$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ADC
=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠BAD+∠ABG
=∠BAD+∠ABG,
∴∠1=∠2,
点评 本题考查三角形内角和综合问题,解题的关键是灵活运用三角形的内角和定理以及三角形的外角性质.本题属于中等题型.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
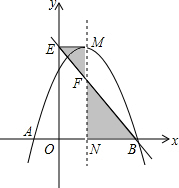 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB,垂足为D,PE⊥AC,垂足为E.
△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB,垂足为D,PE⊥AC,垂足为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com