练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．若25x2=100，则x=±2．

    分析 先将25x2=100，化为x2=4，再根据平方根的定义，求数4的平方根，也就是求一个数x，使得x2=a，则x就是a的平方根，由此即可解决问题．

    解答 解：∵25x2=10，
    ∴x2=4，
    ∴x=±2．
    故答案为±2．

    点评 本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．一元二次方程x2-6x-4=0两根为x1和x2，则x1+x2=6x1x2=-4x1+x2-x1x2=10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．抛物线y=2（x+2）2+1的顶点坐标是（-2，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在平面直角坐标系中，抛物线y=ax2+3x+c交x轴正半轴于点A，点B，交y轴于点C，直线y=$\frac{1}{2}$x-5经过点B、点C．
    （1）求抛物线的解析式；
    （2）点D在x轴上方的抛物线上，DP⊥x轴，垂足为点G，交PD于点P，DG=2GP，求点D的坐标；
    （3）在（2）的条件下，点E在x轴下方的抛物线上，过点E作EF⊥x轴，垂足为点F，连接DE、DF，点H为线段DF的中点，连接GH交线段DE于点K，GK=$\frac{2}{3}$DK时，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

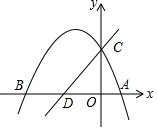    13．如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+bx+c的顶点为（-3，$\frac{25}{4}$），与x轴交于A，B两点（点A在点B的右侧），与y轴交于点C，D是BO的中点，直线DC的解析式为y=kx+4．
    （1）求抛物线的解析式；
    （2）求△ADC的面积；
    （3）点P是抛物线上一个动点（不与点C重合），若S△BDP=S△BDC，求点P的坐标；
    （4）点P是抛物线在第二象限部分图象上一点，连接PD、PC，若点P的横坐标为t，
    ①写出S△CDP关于t的函数关系式；
    ②计算S△CDP的最大值，及此时点P的坐标；
    ③若PD将四边形BPCD的面积分成2：3的两部分，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，线段AB=4，点O是线段AB上的点，点C、D是线段OA、OB的中点，小明很轻松地求得CD=2．他在反思过程中突发奇想：若点O在AB延长线上运动时，原有的结论“CD=2”是仍然成立呢？请帮小明画出图形分析并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

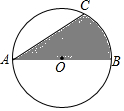    10．如图，AB是⊙O 的直径，C是⊙O 上一点，且AC=$\sqrt{3}$，∠CAB=30°．图中阴影部分的面积是$\frac{\sqrt{3}}{4}$+$\frac{π}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．y=-3x+b上有两点A（a，-2），B（b，3），则a与b的大小关系是a＞b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

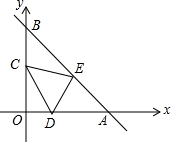    7．已知：如图，直线y=-x+12分别交x轴、y轴于A、B点，将△AOB折叠，使A点恰好落在OB的中点C处，折痕为DE．
    （1）求AD的长；
    （2）求sin∠BEC的值．

    查看答案和解析>>

    同步练习册答案