
分析 (1)先化简,再合并同类项即可求解;
(2)先化简,再计算括号里面的减法,最后计算括号外面的乘法;
(3)本题涉及乘方、绝对值、零指数幂、负整数指数幂、二次根式化简5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)$\sqrt{45}$+$\sqrt{18}$-$\sqrt{8}$+$\sqrt{125}$
=3$\sqrt{5}$+3$\sqrt{2}$-2$\sqrt{2}$+5$\sqrt{5}$
=8$\sqrt{5}$+$\sqrt{2}$;
(2)3$\sqrt{8}$×($\sqrt{54}$-5$\sqrt{2}$-2$\sqrt{6}$)
=6$\sqrt{2}$×(3$\sqrt{6}$-5$\sqrt{2}$-2$\sqrt{6}$)
=6$\sqrt{2}$×($\sqrt{6}$-5$\sqrt{2}$)
=12$\sqrt{3}$-60;
(3)(-1)2013-|-7|+$\sqrt{9}$×($\sqrt{7}$-π)0+(${\frac{1}{5}}$)-1
=-1-7+3×1+5
=-1-7+3+5
=0.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握合并同类项、乘方、绝对值、零指数幂、负整数指数幂、二次根式化简等考点的运算.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
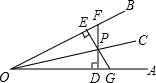 如图,P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,延长DP交OB于点F,延长EP交OA于点G,则图中有三对全等三角形,它们分别是Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG.
如图,P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,延长DP交OB于点F,延长EP交OA于点G,则图中有三对全等三角形,它们分别是Rt△POE和Rt△POD、△PEF和△PDG、△POF和△POG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
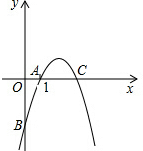 如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.
如图,抛物线y=-x2+5x+n经过点A(1,0),与x轴交于A、C两点,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
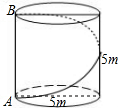 壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?
壁虎在一座油罐的下底边沿A处.它发现在自己的正上方──油罐上边缘的B处有一只害虫.壁虎决定捕捉这只害虫.为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿着一条螺旋路线,从背后对害虫进行突然袭击如图.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问:壁虎沿着螺旋线爬行是最短的路程吗(线段AB除外)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
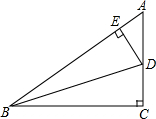 如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.
如图,在△ABC中,∠C=90°,BD平分∠ABC,DE⊥AB于点E,AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com