
分析 (1)令y=0,求出x的值;令x=0,求出y,即可解答;
(2)先求出A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),再代入解析式,即可解答;
(3)取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,由此判定四边形AMA′M′为平行四边形,又知AA′与MM′不垂直,从而平行四边形AMA′M′不是菱形,过点M作MD⊥x轴于点D,求出抛物线的顶点坐标M,根据${S}_{平行四边形AM{A}^{′}{M}^{′}}=2{S}_{△AM{A}^{′}}$,即可解答.
解答 解:(1)令y=0,得x2+5x+4=0,
∴x1=-4,x2=-1,
令x=0,得y=4,
∴A(-4,0),B(-1,0),C(0,4).
(2)∵A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,-4),
∴所求抛物线的函数表达式为y=ax2+bx-4,
将(4,0),(1,0)代入上式,得$\left\{\begin{array}{l}{16a+4b-4=0}\\{a+b-4=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$,
∴y=-x2+5x-4.
(3)如图,取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,
由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,
∴四边形AMA′M′为平行四边形,
又知AA′与MM′不垂直,
∴平行四边形AMA′M′不是菱形,
过点M作MD⊥x轴于点D,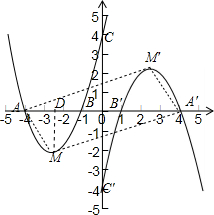
∵y=${x}^{2}+5x+4=(x+\frac{5}{2})^{2}-\frac{9}{4}$,
∴M($-\frac{5}{2},-\frac{9}{4}$),
又∵A(-4,0),A′(4,0)
∴AA′=8,MD=$\frac{9}{4}$,
∴${S}_{平行四边形AM{A}^{′}{M}^{′}}=2{S}_{△AM{A}^{′}}$=$2×\frac{1}{2}×8×\frac{9}{4}=18$
点评 本题考查了二次函数的性质与图象、中心对称、平行四边形的判定、菱形的判定,综合性较强,解决本题的关键是根据中心对称,求出抛物线的解析式,在(3)中注意菱形的判定与数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
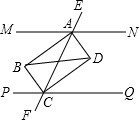 已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.
已知MN∥PQ,同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
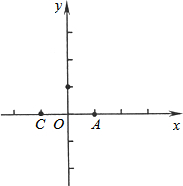 在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).
在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1,使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去.则点P3的坐标为(0,-2);点Pn在y轴上,则点Pn的坐标为(0,0)或(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
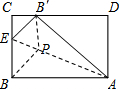 如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.
如图所示,矩形纸片ABCD中,AB=5,AD=4,将纸片折叠,使点D落在边CB上的D′处,折痕为AE,在折痕AE上存在一点P到边CB的距离与到点D的距离相等,则此相等距离为2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
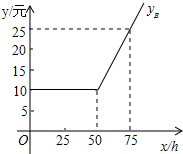 随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.
如图,在平行四边形ABCD中,∠BAD的平分线交BC的延长线于点E,交CD于点G,过点E作EF∥CD,过点G作FG∥EC,EF,FG交于点F.求证:四边形CEFG为菱形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com