
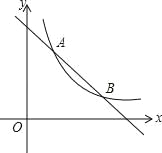
【题目】如图,一次函数 y=﹣x+4 的图象与反比例 y=![]() (k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(k 为常数, 且 k≠0)的图象交于 A(1,a)、B(b,1)两点.
(1)求点 A、B 的坐标及反比例函数的表达式;
(2)在 x 轴上找一点,使 PA+PB 的值最小,求满足条件的点 P 的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将x=1代入直线AB的函数表达式中即可求出点A的坐标,由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式,联立两函数表达式成方程组,通过解方程组即可求出点B的坐标;
(2)作B点关于x轴的对称点B′(2,-1),连接AB’,交x轴于点P,连接PB,由两点之间线段最短可得出此时PA+PB取最小值,根据点A、B′的坐标利用待定系数法可求出直线AB′的函数表达式,再利用一次函数图象上点的坐标特征即可求出点P的坐标.
![]() 在一次函数
在一次函数![]() 的图象上,
的图象上,
![]() ,
,
![]() .
.
![]() 在反比例
在反比例![]() 为常数,且
为常数,且![]() 的图象上,
的图象上,
![]() ,
,
![]() 反比例函数的表达式为
反比例函数的表达式为![]() .
.
联立一次函数与反比例函数关系式成方程组,得:
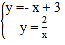 ,解得:
,解得:![]() ,
,
![]() .
.
![]() 作B点关于x轴的对称点
作B点关于x轴的对称点![]() ,连接
,连接![]() ,交x轴于点P,连接PB,如图所示.
,交x轴于点P,连接PB,如图所示.
![]() 点B、
点B、![]() 关于x轴对称,
关于x轴对称,
![]() .
.
![]() 点A、P、
点A、P、![]() 三点共线,
三点共线,
![]() 此时
此时![]() 取最小值.
取最小值.
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
将![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
当![]() 时,
时,![]() ,
,
![]() 满足条件的点P的坐标为
满足条件的点P的坐标为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
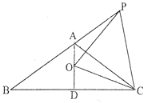
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,
,![]() ,把一条长为2016个单位长度且没有弹性的细线
,把一条长为2016个单位长度且没有弹性的细线![]() 线的粗细忽略不计
线的粗细忽略不计![]() 的一端固定在点A处,并按
的一端固定在点A处,并按![]() 的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是
的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是![]()
![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
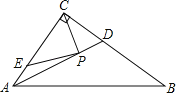
【题目】如图,在R△ABC中,∠ACB=90°,AC=6,BC=8,E为AC上一点,且AE=![]() ,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )
,AD平分∠BAC交BC于D.若P是AD上的动点,则PC+PE的最小值等于( )
A.![]() B.
B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
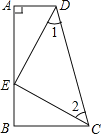
(1)求证:△ADE≌△BEC;
(2)若AD=3,AB=9,求△ECD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
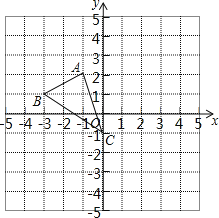
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴的正半轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC.有下列结论:①abc<0;②3b+4c<0;③c>﹣1;④关于x的方程ax2+bx+c=0有一个根为﹣![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
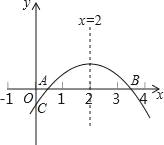
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com