
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
【答案】(1)生物园的宽为![]() 米,长为
米,长为![]() 米;(2)不能围成面积为
米;(2)不能围成面积为![]() 平方米的生物园,见解析
平方米的生物园,见解析
【解析】
(1)设垂直于墙的一边长为x米,则平行于墙的一边长为(16-2x)米,根据长方形的面积公式结合生物园的面积为30平方米,即可得出关于x的一元二次方程,解之取其较大值即可得出结论;
(2)设垂直于墙的一边长为y米,则平行于墙的一边长为(16-2y)米,根据长方形的面积公式结合生物园的面积为35平方米,即可得出关于y的一元二次方程,由根的判别式△<0可得出该方程无解,进而可得出不能围成面积为35平方米的生物园.
解:(1)设生物园的宽为![]() 米,那么长为
米,那么长为![]() 米,依题意得:
米,依题意得:
![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,不符合题意,舍去
,不符合题意,舍去
∴![]() ,
,
答:生物园的宽为![]() 米,长为
米,长为![]() 米.
米.
(2)设生物园的宽为![]() 米,那么长为
米,那么长为![]() 米,依题意得:
米,依题意得:
![]() ,
,
∵![]() ,
,
∴此方程无解,
∴不能围成面积为![]() 平方米的生物园.
平方米的生物园.


科目:初中数学 来源: 题型:
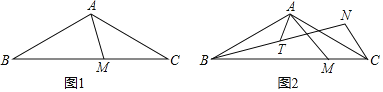
【题目】在△ABC中,AB=AC,∠BAC=120°,M为BC边上一动点(M不与B、C重合)
(1)如图1,若∠MAC=45°,求![]() ;
;
(2)如图2,将CM绕点C顺时针旋转60°至CN,连接BN,T为BN的中点,连接AT.
①求证:AM=2AT;
②当AB=AC=2时,直接写出CM+4AT的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:若关于x的一元二次方程ax2+bx+c=0的两个非零实数根分别为x1,x2,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
解决下列问题:已知关于x的一元二次方程(x+n)2=6x有两个非零不等实数根x1,x2,设m=![]() ,
,
(Ⅰ)当n=1时,求m的值;
(Ⅱ)是否存在这样的n值,使m的值等于![]() ?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 中
中![]() 边的中点,
边的中点,![]() 于
于![]() ,以
,以![]() 为直径的
为直径的![]() 经过
经过![]() ,连接
,连接![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是
是![]() 的切线.其中正确的结论是( )
的切线.其中正确的结论是( )
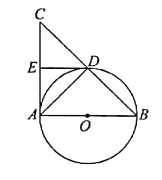
A.①②B.①②③C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() ,其顶点为A.
,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)直线BC平行于x轴,交这条抛物线于B、C两点(点B在点C左侧),且![]() ,求点B坐标.
,求点B坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .平行四边形
.平行四边形![]() 的顶点
的顶点![]() 在线段
在线段![]() 上(点
上(点![]() 在
在![]() 的左边),顶点
的左边),顶点![]() 分别在线段
分别在线段![]() 和
和![]() 上.
上.
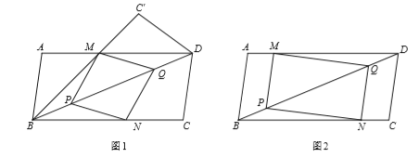
(1)求证:![]() ;
;
(2)如图1,将![]() 沿直线
沿直线![]() 折叠得到
折叠得到![]() ,当
,当![]() 恰好经过点
恰好经过点![]() 时,求证:四边形
时,求证:四边形![]() 是菱形;
是菱形;
(3)如图2,若四边形![]() 是矩形,且
是矩形,且![]() ,求
,求![]() 的长.(结果中的分母可保留根式)
的长.(结果中的分母可保留根式)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为吸引市民组团去风景区旅游,观光旅行社推出了如下收费标准:

某单位员工去风景区旅游,共支付给旅行社旅游费用10500元,请问该单位这次共有多少员工去风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC
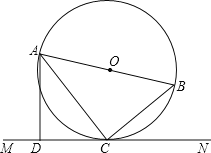
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com